Sur ce thème
Linéarité
La linéarité évalue l'évolution du biais moyen sur l'étendue d'utilisation attendue du système de mesure. La linéarité indique si l'instrumentation présente la même exactitude pour toutes les tailles d'objets mesurées.
Formule
Linéarité = | Pente | * Variation du procédé
%Linéarité
La valeur %Linéarité est la linéarité exprimée sous forme de pourcentage de la variation globale du procédé.
Formule
%Linéarité = (Linéarité / Variation du procédé) * 100
valeur de p de linéarité de l'instrumentation
Utilisez les valeurs de p pour la constante et la pente afin de tester si la pente est égale à 0 et si la constante est égale à 0.
La valeur de p se définit comme l'aire sous la loi d'échantillonnage à droite de la |statistique de test| + et l'aire sous la loi d'échantillonnage à gauche de la |statistique de test| -. Minitab utilise la loi T avec γ DL et la statistique t pour calculer la valeur de p.
- Pour la constante, si la valeur de p est supérieure à la valeur d'α, vous ne pouvez pas rejeter l'hypothèse nulle et vous concluez que le biais de toutes les valeurs de référence est égal à 0.
- Pour la pente, si la valeur de p est supérieure à la valeur d'α, vous ne pouvez pas rejeter l'hypothèse nulle et vous concluez que le système de mesure présente le même biais pour toutes les valeurs de référence (absence de linéarité).
- Pour la constante, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le biais de toutes les valeurs de référence n'est pas égal à 0.
- Pour la pente, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le système de mesure ne présente pas le même biais pour toutes les valeurs de référence (linéarité présente).
R carré
R carré (R2) est le coefficient de détermination, qui permet de vérifier si la droite d'ajustement modélise les données correctement. La valeur R carré (R2) représente la proportion de variation dans le biais, qui est expliquée par la relation linéaire entre les biais et les valeurs de référence.
Formule
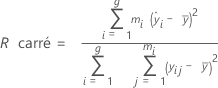
Notation
| Terme | Description |
|---|---|
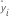 | ième réponse ajustée |
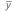 | biais moyen |
| yij | biais de la jème mesure de la ième pièce |
| g | nombre de pièces |
| mi | nombre de répétitions de la ième pièce |
S
S est une estimation de σ, l'écart type autour de la droite de régression.
Formule
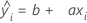
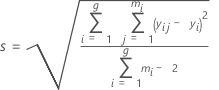
Notation
| Terme | Description |
|---|---|
| xi | valeur de référence de la pièce i |
| yij | biais de la jème mesure de la ième pièce |
| g | nombre de pièces |
| mi | nombre de répétitions de la ième pièce |
Pente, Constante
La droite de régression du diagramme des valeurs de biais en fonction de la référence prend la forme suivante :
Formules
Pente de la droite de régression (a) :
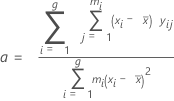
Ordonnée à l'origine de la droite de régression (b) :

Notation
| Terme | Description |
|---|---|
| a | pente |
| b | ordonnée à l'origine |
| xi | valeur de référence de la pièce i |
 | valeur de référence moyenne pour toutes les pièces |
| yij | biais de la jème mesure de la ième pièce |
| g | nombre de pièces |
| mi | nombre de répétitions de la ième pièce |
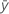 | moyenne du biais globale |
