Sur ce thème
Diagramme de biais en fonction de la référence
Utilisez le diagramme du biais en fonction de la valeur de référence pour observer le degré de variation des valeurs de biais pour chaque pièce. Les points bleus représentent les valeurs de biais pour chaque valeur de référence. Le carré rouge représente la valeur de biais moyenne pour chaque valeur de référence. La droite est la droite de régression des moindres carrés ajustée à la moyenne des écarts.
Interprétation
L'idéal serait que les écarts pour chaque pièce soient proches de 0 et que la droite d'ajustement soit horizontale.
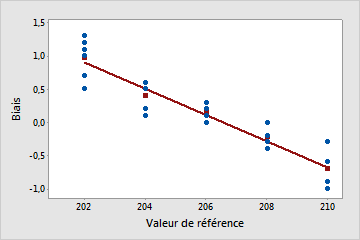
La linéarité semble être un problème
La ligne tracée est inclinée. Dans cet exemple, les mesures des plus petites pièces sont supérieures aux valeurs de pièces de référence correspondantes. Les mesures des plus grandes pièces ont tendance à être inférieures aux valeurs de pièces de référence correspondantes.
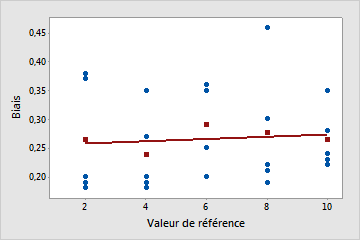
La linéarité ne semble pas être un problème
La ligne tracée est pratiquement horizontale, ce qui indique que le biais moyen est relativement constant et ne dépend pas de la valeur de référence. Dans cet exemple, les mesures de toutes les pièces sont supérieures aux mesures de pièce de référence correspondantes.
Coeff
Les coefficients sont des chiffres de la droite de régression du diagramme du biais en fonction de la valeur de référence.
La forme générale de cette droite de régression des moindres carrés est la suivante :
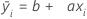
Le terme b représente le coefficient de constante. Il indique le point d'intersection entre la droite d'ajustement et l'axe des y.
Le terme a représente le coefficient de pente. La pente d'une droite désigne son inclinaison et correspond au changement de l'axe des y par rapport au changement de l'axe des x.
Interprétation
Lorsque le coefficient de pente, a, est très faible, la pente est presque horizontale. Ainsi, le biais est relativement constant entre les valeurs de référence, et la linéarité n'est pas un problème significatif. Des valeurs absolues plus élevées du coefficient de pente, |a|, indiquent une pente plus importante de la droite. Si la valeur de p de la pente est inférieure à alpha, la linéarité est significative.
En l'absence de linéarité significative, des valeurs absolues plus élevées du coefficient de constante, |b|, indiquent un biais supérieur. En présence d'une linéarité significative, vous devez examiner les valeurs de biais individuelles.
Coef ErT
L'erreur type de l'estimation d'un coefficient de régression mesure le degré de précision de l'estimation du modèle de la valeur inconnue du coefficient. L'erreur type du coefficient est toujours positive.
Interprétation
Vous pouvez utiliser l'erreur type du coefficient pour mesurer la précision de l'estimation du coefficient. Plus l'erreur type est petite, plus l'estimation est précise. Si vous divisez le coefficient par son erreur type, vous obtiendrez une valeur de T. Si la valeur de p associée à la valeur de T est inférieure à votre niveau d'α, vous concluez que le coefficient est significativement différent de 0.
valeur de p de linéarité de l'instrumentation
- P pour la constante : utilisez cette valeur pour tester si la constante de la droite de linéarité est égale à 0.
- P pour la pente : utilisez cette valeur pour tester si la pente de la droite de linéarité est égale à 0.
Interprétation
- Pour la constante, si la valeur de p est supérieure à la valeur d'α, vous ne pouvez pas rejeter l'hypothèse nulle et vous concluez que le biais de toutes les valeurs de référence est égal à 0.
- Pour la pente, si la valeur de p est supérieure à la valeur d'α, vous ne pouvez pas rejeter l'hypothèse nulle et vous concluez que le système de mesure présente le même biais pour toutes les valeurs de référence (absence de linéarité).
- Pour la constante, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le biais de toutes les valeurs de référence n'est pas égal à 0.
- Pour la pente, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le système de mesure ne présente pas le même biais pour toutes les valeurs de référence (linéarité présente).
S et R carré
Les mesures S et R carré (R2) évaluent l'ajustement du modèle aux données.
S est une estimation de σ, l'écart type autour de la droite de régression.
La valeur R carré (R2) représente la proportion de variation dans le biais, qui est expliquée par la relation linéaire entre les biais et les valeurs de référence.
Interprétation
Des valeurs inférieures de S indiquent une variabilité inférieure dans les estimations du biais. R2 est comprise entre 0 et 100 %. En général, plus la valeur R2 est élevée, plus le modèle est ajusté à vos données.
Linéarité, %Linéarité
La linéarité évalue l'évolution du biais moyen sur l'étendue d'utilisation attendue du système de mesure. La linéarité indique si votre instrumentation présente la même exactitude (le même biais) parmi l'ensemble des valeurs de référence.
La valeur %Linéarité est la linéarité exprimée sous forme de pourcentage de la variation du procédé.
Interprétation
Pour interpréter la linéarité de vos données, déterminez si le biais change d'une valeur de référence à une autre. Si les données ne forment pas de ligne horizontale sur un nuage de points, la linéarité est alors présente. Idéalement, la droite d'ajustement est horizontale et proche de 0.

La linéarité semble être un problème
La ligne tracée est inclinée. Dans cet exemple, les mesures des plus petites pièces sont supérieures aux valeurs de pièces de référence correspondantes. Les mesures des plus grandes pièces ont tendance à être inférieures aux valeurs de pièces de référence correspondantes.

La linéarité ne semble pas être un problème
La ligne tracée est pratiquement horizontale, ce qui indique que le biais moyen est relativement constant et ne dépend pas de la valeur de référence. Dans cet exemple, les mesures de toutes les pièces sont supérieures aux mesures de pièce de référence correspondantes.
Pour une instrumentation qui mesure les pièces de manière régulière, la valeur %Linéarité est proche de zéro.
Biais, %Biais
Le biais est calculé comme la différence entre la valeur du standard connue d'une pièce de référence et la moyenne observée des mesures.Le biais est une mesure de l'exactitude d'un système de mesure.
La valeur %Biais est le biais exprimé sous forme de pourcentage de la variabilité du procédé.
Interprétation
- Un biais positif indique que l'instrumentation surestime.
- Un biais négatif indique que l'instrumentation sous-estime.
Pour une instrumentation qui mesure avec exactitude, la valeur %Biais est petite.
Valeur de p pour le biais de l'instrumentation
- P pour le biais moyen : utilisez cette valeur pour tester si le biais moyen est égal à 0.
- P pour chaque valeur de référence : utilisez cette valeur pour tester si le biais est égal à 0 à chaque valeur de référence.
Interprétation
- Pour chaque valeur de référence, si la valeur de p est supérieure à la valeur d'α, vous ne pouvez pas rejeter l'hypothèse nulle et vous concluez que le biais est égal à 0.
- Pour le biais moyen, si la valeur de p est supérieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le biais moyen est égal à 0.
- Pour chaque valeur de référence, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le biais n'est pas égal à 0.
- Pour le biais moyen, si la valeur de p est inférieure à la valeur d'α, vous rejetez l'hypothèse nulle et vous concluez que le biais moyen n'est pas égal à 0.
