Sur ce thème
Composantes de la variance
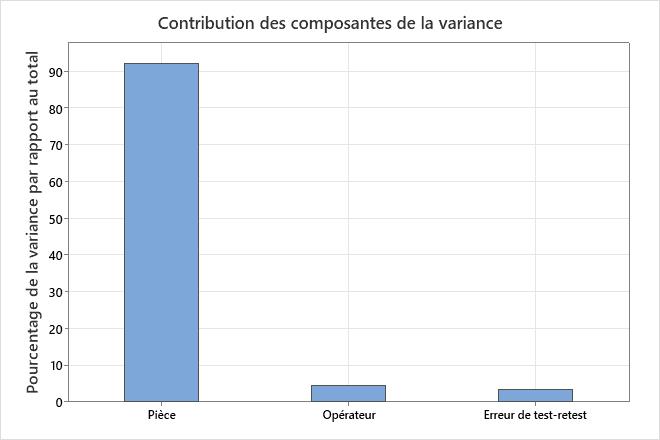
Le graphique Contribution des composantes de la variance et le tableau Composantes de la variance montrent la variation provenant de différentes sources.
Interprétation
Utilisez les composantes de variance pour évaluer la variation de chaque source. La variance test-retest et la variance opérateur sont des erreurs de mesure. La variation de la pièce représente la gamme de pièces de l’étude. La variance totale est la somme des autres composantes. Si l’analyse inclut l’interaction, le degré d’erreur de mesure dépend de la partie mesurée par l’opérateur.
Dans un système de mesure acceptable, la composante la plus importante de la variation est la variation de la pièce. Si la variation test-retest et la variation de l’opérateur contribuent à une grande quantité de variation, recherchez la source du problème et prenez des mesures correctives.
Composantes de la variance
| Source | Variance | Total en % | Ecart type |
|---|---|---|---|
| Erreur de test-retest (répétabilité) | 0,03997 | 3,394 | 0,19993 |
| Opérateur (reproductibilité) | 0,05146 | 4,368 | 0,22684 |
| Pièce (variation du produit) | 1,08645 | 92,238 | 1,04233 |
| Total | 1,17788 | 100,000 | 1,08530 |
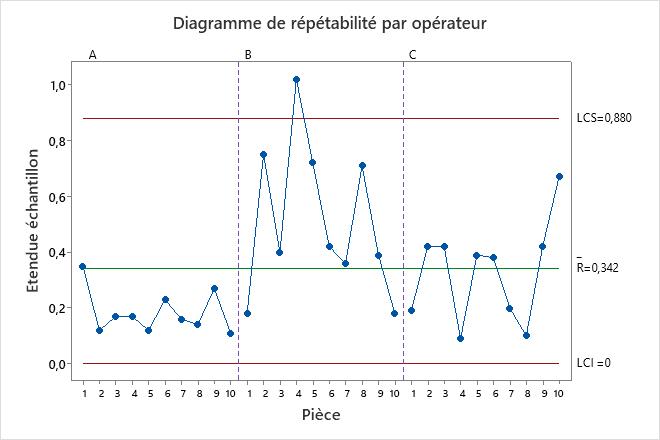
Graphique de répétabilité
Le graphique de répétabilité est un graphique de contrôle des plages qui affiche la cohérence de l’opérateur.
- Points relevés
- Pour chaque opérateur, la plage d’échantillonnage correspond à la différence entre les mesures les plus grandes et les plus petites de chaque pièce. Utilisez les plages d’échantillonnage pour évaluer la cohérence de l’opérateur.
- Ligne centrale (R barre)
- Moyenne générale pour le procédé (c'est-à-dire, moyenne de toutes les étendues d'échantillon).
- Limites de contrôle (LCI et LCS)
- Degré de variation auquel vous pouvez vous attendre pour les étendues d'échantillon. Pour calculer les limites de contrôle, Minitab utilise la variation à l'intérieur des échantillons.
Remarque
Si chaque opérateur mesure chaque pièce 9 fois ou plus, Minitab affiche les écarts-types sur le graphique au lieu des plages.
Interprétation
Plus la plage moyenne est petite, plus la variation par rapport au système de mesure est faible. Un point situé au-delà de la limite de contrôle supérieure (LCS) indique que l'opérateur ne mesure pas les pièces de façon cohérente. Le calcul de l’UCL comprend le nombre de mesures par pièce par chaque opérateur, et la variation de la pièce. Si les opérateurs mesurent les pièces de façon cohérente, l'étendue entre les mesures les plus hautes et les plus basses est faible par rapport à la variation de l'étude et les points sont maîtrisés.
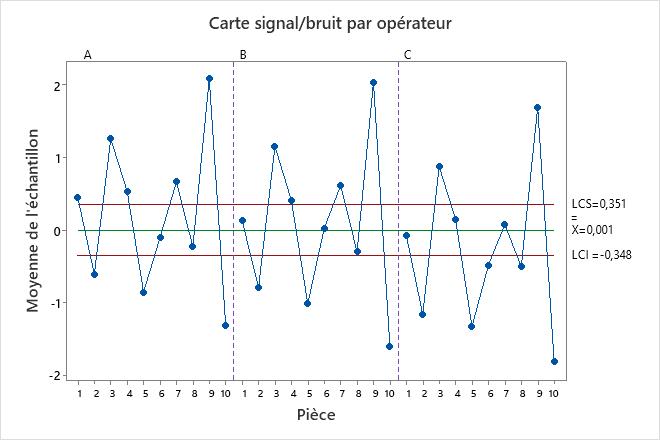
Graphique signal/bruit par opérateur
Le graphique compare la variation de la pièce à la composante test-retest.
- Points relevés
- Mesure moyenne de chaque pièce, représentée par chaque opérateur.
- Ligne centrale (
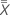 )
) - Moyenne globale de toutes les mesures des pièces par tous les opérateurs.
- Limites de contrôle (LCI et LCS)
- Les limites de contrôle sont basées sur l'estimation de répétabilité et sur le nombre de mesures dans chaque moyenne.
Interprétation
Les pièces choisies pour une étude doivent représenter l’ensemble des pièces possibles. Ainsi, ce graphique devrait indiquer plus de variation entre les moyennes des pièces que ce que l’on attend de la seule variation test-retest.
L'idéal est que le graphique possède des limites de contrôle étroites avec de nombreux points hors contrôle indiquant un système de mesure avec une faible variation.
Graphique de parallélisme
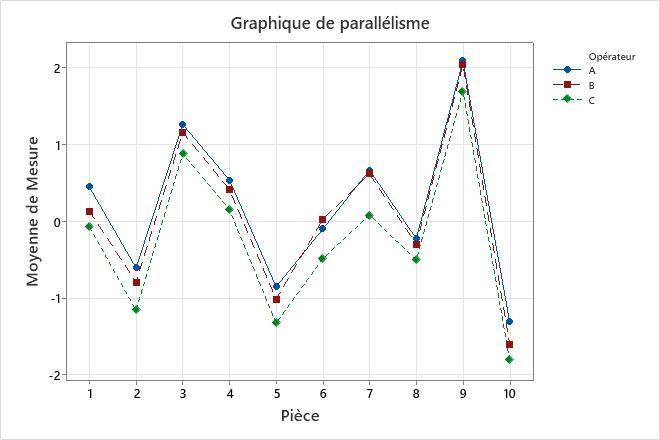
Le graphique de parallélisme affiche les mesures moyennes de chaque opérateur pour chaque pièce. Chaque ligne relie les moyennes d'un opérateur unique.
Le graphique montre l’interaction entre deux sources de variation : les pièces et les opérateurs. Une interaction survient lorsque l'effet d'un facteur dépend d'un autre facteur.
Interprétation
Les lignes qui coïncident indiquent que les opérateurs mesurent de façon similaire. Les lignes qui ne sont pas parallèles ou qui se croisent indiquent que la capacité d'un opérateur à mesurer une pièce dépend invariablement de la pièce mesurée. Une ligne qui est invariablement supérieure ou inférieure aux autres indique qu'un opérateur ajoute un biais à la mesure en sous-estimant ou en surestimant invariablement.
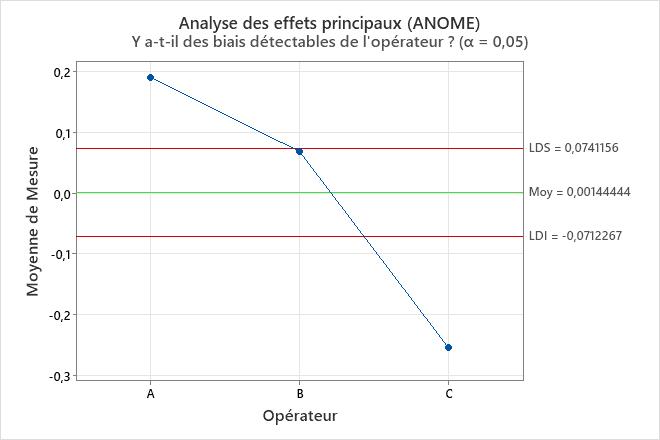
Graphique de l’analyse des effets principaux (ANOME)
Le graphique compare les mesures moyennes pour les opérateurs.
- Points relevés
- La mesure moyenne de toutes les pièces pour chaque opérateur.
- Ligne centrale (moyenne)
- Moyenne globale de toutes les mesures des pièces par tous les opérateurs.
- Limites de décision (LDL et CUL)
- Les limites sont basées sur l’estimation test-retest et le nombre de mesures dans chaque moyenne.
Interprétation
Les points en dehors des limites de décision indiquent que différents opérateurs ajoutent un biais aux mesures. Idéalement, les points sont tous à l’intérieur des limites de décision pour indiquer que les moyennes globales des opérateurs sont similaires.
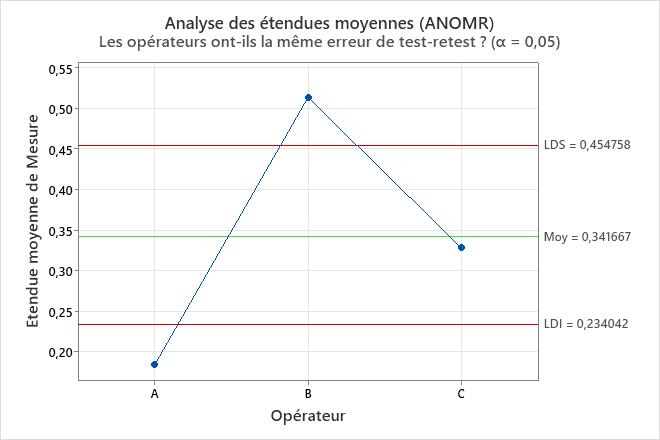
Graphique de l’analyse des étuendes moyennes (ANOMR)
Le graphique compare la plage moyenne des mesures pour les opérateurs.
- Points relevés
- Moyenne des étuendes de mesures pour chaque pièce pour chaque opérateur.
- Ligne centrale (moyenne)
- Moyenne globale de toutes les gammes par tous les opérateurs.
- Limites de décision (LDL et CUL)
- Les limites sont basées sur l’estimation test-retest.
Interprétation
Les points en dehors des limites de décision indiquent que certains opérateurs mesurent plus ou moins régulièrement que d’autres. Idéalement, les points sont tous à l’intérieur des limites de décision pour indiquer que les plages globales des opérateurs sont similaires.
Statistiques et directives de classification EMP
Les statistiques EMP classent le système de mesure de la meilleure note de première classe à la pire note de quatrième classe. Les classes correspondent au coefficient de corrélation intraclasse. Concrètement, le coefficient explique dans quelle mesure le système de mesure détecte un décalage d’au moins 3 écarts-types dans la moyenne du processus. Les systèmes de mesure de première et de deuxième classe ont généralement une forte probabilité de détecter de tels changements avec un nombre limité de tests et de sous-groupes sur une carte de contrôle. Pour les systèmes de mesure de troisième classe, l’analyse typique ajoute des tests à la carte de contrôle pour augmenter la probabilité de détecter un changement dans la moyenne du processus. Un système de mesure de quatrième classe nécessite généralement une amélioration pour surveiller un processus ou pour des activités d’amélioration du processus.
La classification concerne également l’atténuation des signaux du processus. L’atténuation est la quantité de changement qui est confondue avec l’erreur de mesure. Pour un système de mesure qui atténue 50 % d’une variation, une variation de 2 écarts-types est susceptible d’apparaître comme une variation de 1 écart-type.
- Erreur de test-retest
- La variabilité des mesures lorsqu’un même opérateur mesure plusieurs fois la même pièce. Plus la valeur est petite, meilleures sont les performances du système de mesure.
- Degrés de liberté
- Degrés de liberté (DF) pour l’estimation de l’erreur test-retest. En général, DF mesure la quantité d’informations disponibles pour calculer l’erreur.
- Erreur probable
- L’incertitude pour une seule mesure. L’analyse compare l’erreur probable à l’incrément de mesure dans le tableau Résolution effective des mesures pour conclure si la précision des mesures est fiable. Wheeler (2006) 1 décrit les méthodes d’utilisation de l’erreur probable pour déterminer les limites de spécification d’un procédé, compte tenu de la performance du système de mesure.
- Corrélation intraclasse
- Le coefficient de corrélation intraclasse compare la variation totale à la variation de la pièce. Des valeurs plus proches de 1 indiquent moins de variation par rapport au système de mesure.
- Pas de biais
- Sans biais, le coefficient décrit les performances du système de mesure si tous les opérateurs mesurent les pièces de la même manière en moyenne.
- Avec biais
- Avec biais, le coefficient décrit les performances du système de mesure avec les différences entre les opérateurs.
- Avec biais et interaction
- Lorsque l’analyse détecte que différents opérateurs mesurent différentes parties différemment, les résultats incluent la corrélation intraclasse avec le biais et l’interaction. Le coefficient décrit les performances du système de mesure lorsque différents opérateurs mesurent différentes pièces.
- Impact du biais
- Différence entre le coefficient intraclasse avec biais et le coefficient pas de biais. Plus la valeur est petite, moins les différences entre opérateurs contribuent à la variation des mesures.
- Impact du biais et de l'interaction
- Différence entre le coefficient intraclasse avec biais et interaction et le coefficient pas de biais. Plus la valeur est petite, moins les différences dans la façon dont les différents opérateurs mesurent les différentes parties contribuent à la variation des mesures.
Statistiques EMP
| Statistique | Valeur | Classement |
|---|---|---|
| Erreur de test-retest | 0,1999 | |
| Degrés de liberté | 78,0000 | |
| Erreur probable | 0,1349 | |
| Corrélation intraclasse (pas de biais) | 0,9645 | Première classe |
| Corrélation intraclasse (avec biais) | 0,9224 | Première classe |
| Impact du biais | 0,0421 |
Indications en matière de classement
| Classement | Corrélation intraclasse | Atténuation des signaux de procédé | Probabilité d'avertissement, test 1* | Probabilité d'avertissement, tests* |
|---|---|---|---|---|
| Première classe | 0,80 - 1,00 | Moins de 11% | 0,99 - 1,00 | 1,00 |
| Deuxième classe | 0,50 - 0,80 | 11 - 29% | 0,88 - 0,99 | 1,00 |
| Troisième classe | 0,20 - 0,50 | 29 - 55% | 0,40 - 0,88 | 0,92 - 1,00 |
| Quatrième classe | 0,00 - 0,20 | Supérieur à 55% | 0,03 - 0,40 | 0,08 - 0,92 |
Résolution efficace des mesures
Les statistiques sur la résolution décrivent à quel point vous pouvez faire confiance à la précision enregistrée des mesures.
- Erreur probable (PE)
- L’incertitude pour une seule mesure. L’analyse compare l’erreur probable à l’incrément de mesure dans le tableau Résolution effective des mesures pour conclure si la précision des mesures est fiable. Wheeler (2006)1 décrit des méthodes permettant d’utiliser l’erreur probable pour déterminer les limites de spécification d’un procédé, compte tenu de la performance du système de mesure.
- Limite inférieure de l’incrément (0,1 * PE)
- Limite inférieure pour savoir quand l’incrément de mesure est fiable. Lorsque l’incrément de mesure est inférieur à la limite inférieure de l’incrément, il faut sérieusement envisager d’enregistrer les mesures avec moins de précision.
- Incrément effectif le plus petit (0,22 * PE)
- Estimation de la précision de la mesure que le système est susceptible de produire. Lorsque l’incrément de mesure est inférieur au plus petit incrément effectif, demandez-vous s’il convient d’enregistrer les mesures avec moins de précision.
- Incrément de mesure du courant
- Une estimation à partir des données ou d’une valeur spécifiée qui explique la précision des mesures enregistrées. Par exemple, pour les valeurs 1,1; 1,4 et 1,9, l’analyse détermine que l’incrément est de 0,1, car les mesures incluent la place des dixièmes.
- Incrément effectif le plus élevé (2,2 * PE)
- Estimation de la précision de la mesure que le système est susceptible de produire. Lorsque l’incrément de mesure est supérieur à l’incrément effectif le plus élevé, demandez-vous s’il convient d’enregistrer les mesures avec plus de précision.
Probabilités de mauvais classement
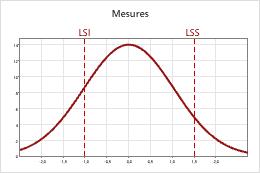
Lorsque vous indiquez au moins une limite de spécification, Minitab peut calculer les probabilités de mauvais classement d'un produit. Etant donné la variation d'instrumentation, la valeur mesurée de la pièce n'est pas toujours égale à sa valeur réelle. L'écart entre la valeur mesurée et la valeur réelle crée une possibilité de mauvais classement de la pièce.
- Probabilité conjointe
- Utilisez la probabilité conjointe lorsque vous ne possédez pas de connaissances préalables sur le caractère acceptable des pièces. Prenons l'exemple d'un échantillon prélevé dans une chaîne de production sans que vous sachiez si telle ou telle pièce est de bonne ou de mauvaise qualité. Vous pouvez effectuer un mauvais classement de deux façons :
- Probabilité que la pièce soit mauvaise et que vous l'acceptiez.
- Probabilité que la pièce soit bonne et que vous la rejetiez.
- Probabilité conditionnelle
- Utilisez l'option Probabilité conditionnelle lorsque vous possédez des connaissances préalables sur le caractère acceptable des pièces. Prenons l'exemple d'un échantillon prélevé dans une pile de pièces à réusiner ou dans une pile de produits prêts à être expédiés et considérés comme étant de bonne qualité. Vous pouvez effectuer un mauvais classement de deux façons :
- Probabilité que vous acceptiez une pièce échantillonnée dans une pile de mauvais produits devant être réusinés (également appelée acceptation à tort).
- Probabilité que vous rejetiez une pièce échantillonnée dans une pile de bons produits sur le point d'être expédiés (également appelée rejet à tort).
Interprétation
Probabilités conjointes de mauvais classement
| Description | Probabilité |
|---|---|
| Une pièce sélectionnée de manière aléatoire est incorrecte mais acceptée | 0,037 |
| Une pièce sélectionnée de manière aléatoire est correcte mais rejetée | 0,055 |
Probabilités conditionnelles de mauvais classement
| Description | Probabilité |
|---|---|
| Une pièce d'un groupe de produits incorrects est acceptée | 0,151 |
| Une pièce d'un groupe de produits corrects est rejetée | 0,073 |
La probabilité conjointe qu'une pièce soit mauvaise et que vous l'acceptiez est de 0,037. La probabilité conjointe qu'une pièce soit bonne et que vous la rejetiez est de 0,055.
La probabilité conditionnelle d'une acceptation à tort, c'est-à-dire que vous acceptiez une pièce pendant la réinspection alors qu'elle est en réalité hors spécification, est de 0,151. La probabilité conditionnelle d'un rejet à tort, c'est-à-dire que vous rejetiez une pièce pendant la réinspection alors qu'elle est en réalité dans les spécifications, est de 0,073.
