Exemple de Evaluer le processus de mesure (EMP croisé)

Interpréter des résultats

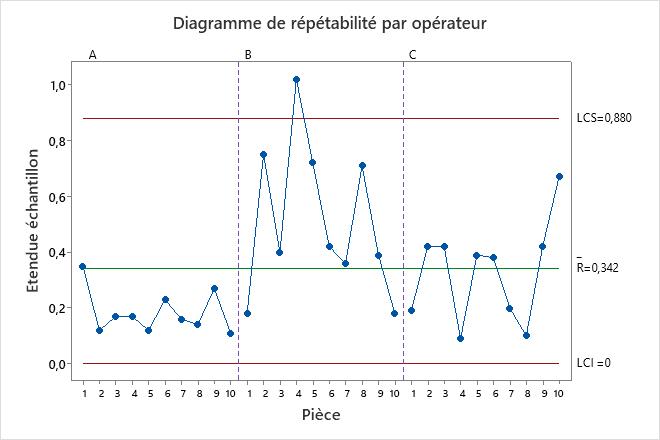
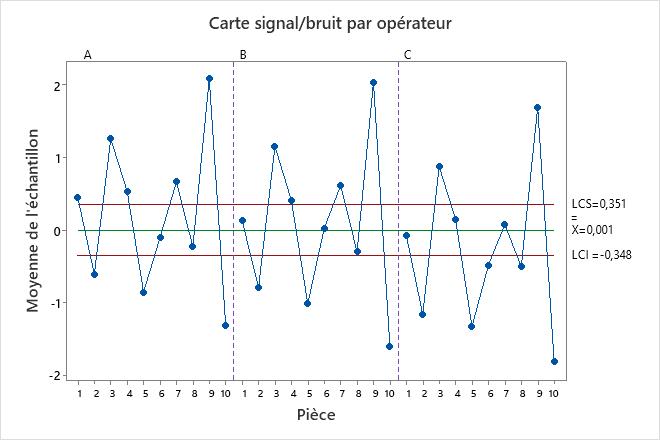
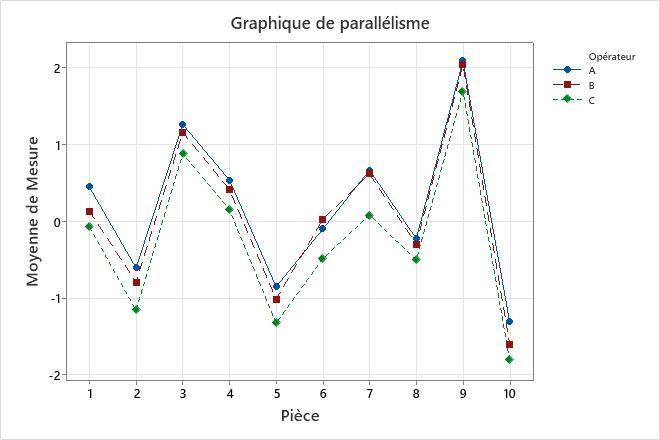
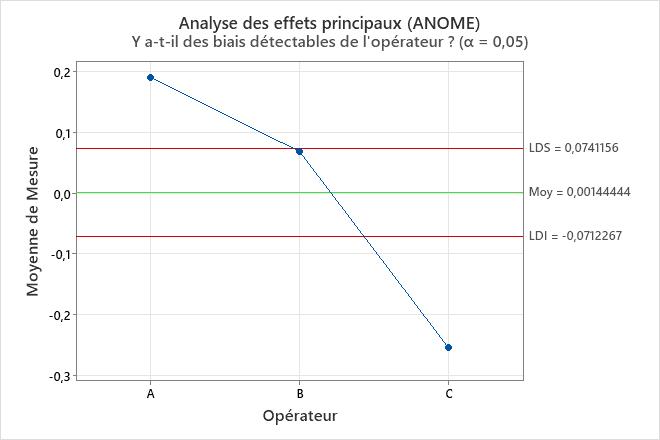
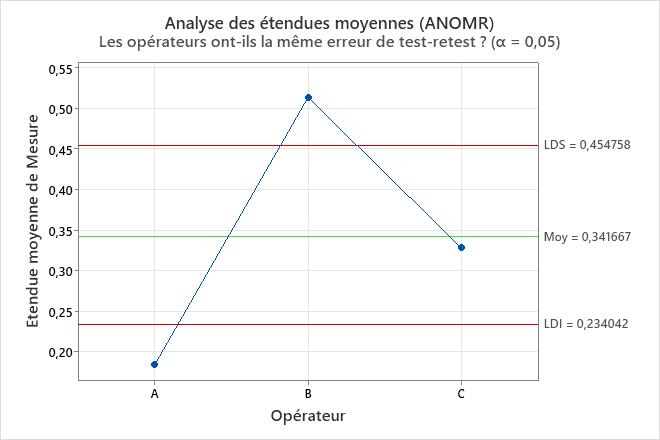
Le tableau des composantes de la variance et les graphiques montrent les possibilités d’amélioration du système de mesure. Par exemple, le diagramme de répétabilité a un point en dehors des limites de contrôle. Examinez ce point pour identifier les problèmes de mesure potentiels. Les points situés en dehors des limites de décision sur le tracé Analyse des effets principaux et le tracé Analyse des plages moyennes montrent que les opérateurs mesurent les pièces différemment. Étudiez la façon dont les opérateurs mesurent les pièces pour améliorer le système de mesure. Le diagramme de parallélisme donne un aperçu des différences entre les opérateurs. Dans ces données, le tracé de parallélisme montre que l’opérateur C a la mesure moyenne la plus faible pour chaque pièce.

Le tableau des Lignes directrices de classification donne les probabilités d’avertissement pour qu’un diagramme à barres X ait un point hors de contrôle à l’intérieur de dix sous-groupes pour l’épreuve 1 ou pour les épreuves 1, 5, 6 et 8. Des systèmes de mesure de première et de deuxième classe sont généralement suffisants pour les activités d’amélioration des processus avec un diagramme à barres X qui utilise le test 1. Des systèmes de mesure de troisième classe sont généralement suffisants pour les activités d’amélioration des processus avec un diagramme à barres X qui utilise les règles 1, 5, 6 et 8. Dans ces données, les statistiques EMP montrent que le système de mesure est de première classe. Même si le système de mesure présente des possibilités d’amélioration, il est suffisant pour de nombreuses activités d’amélioration des processus.

Le tableau Résolution effective des mesures compare la précision des mesures à l’erreur probable du système de mesure. Dans ces données, les mesures contiennent un centième de place, mais l’erreur probable est supérieure à un dixième. Les résultats recommandent que les mesures aillent à la dixième place plutôt qu’à la centième place. L’ingénieur prévoit d’arrondir les mesures, puis d’examiner les nouvelles statistiques EMP pour vérifier que les conclusions sont les mêmes.

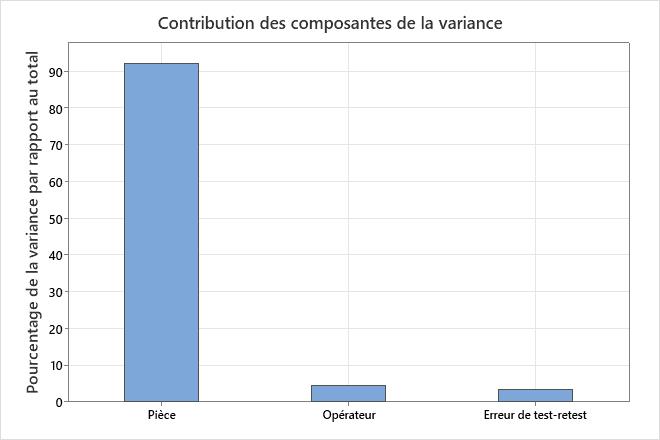
Composantes de la variance

Source	Variance	Total en %	Ecart type
Erreur de test-retest (répétabilité)	0,03997	3,394	0,19993
Opérateur (reproductibilité)	0,05146	4,368	0,22684
Pièce (variation du produit)	1,08645	92,238	1,04233
Total	1,17788	100,000	1,08530

Statistiques EMP

Statistique	Valeur	Classement
Erreur de test-retest	0,1999
Degrés de liberté	78,0000
Erreur probable	0,1349
Corrélation intraclasse (pas de biais)	0,9645	Première classe
Corrélation intraclasse (avec biais)	0,9224	Première classe
Impact du biais	0,0421

Indications en matière de classement

Classement	Corrélation intraclasse	Atténuation des signaux de procédé	Probabilité d'avertissement, test 1*	Probabilité d'avertissement, tests*
Première classe	0,80 - 1,00	Moins de 11%	0,99 - 1,00	1,00
Deuxième classe	0,50 - 0,80	11 - 29%	0,88 - 0,99	1,00
Troisième classe	0,20 - 0,50	29 - 55%	0,40 - 0,88	0,92 - 1,00
Quatrième classe	0,00 - 0,20	Supérieur à 55%	0,03 - 0,40	0,08 - 0,92

Résolution efficace des mesures

Source	Valeur
Erreur probable (PE)	0,134853
Limite inférieure de l'incrément (0,1 * PE)	0,013485
Incrément effectif le plus petit (0,22 * PE)	0,029668
Incrément de mesure actuel	0,010000
Incrément effectif le plus élevé (2,2 * PER)	0,296676