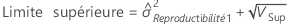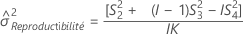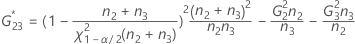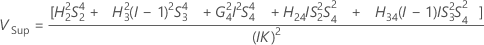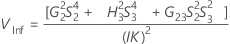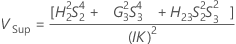Sur ce thème
- Règles et notation communes des intervalles de confiance de R&R de l'instrumentation
- Intervalle de confiance des composantes de la variance de répétabilité
- Intervalle de confiance des composantes de la variance de reproductibilité (ou Opérateur)
- Intervalle de confiance des composantes de la variance du terme Opérateur
- Intervalle de confiance des composantes de la variance d'interaction
- Intervalle de confiance des composantes de la variance de l'instrumentation totale
- Intervalle de confiance des composantes de variance de pièce à pièce
- Intervalle de confiance des composantes de la variance totale
Règles et notation communes des intervalles de confiance de R&R de l'instrumentation
Pour toutes les composantes de variance, les bornes inférieure et supérieure des composantes de variance ne doivent pas être des valeurs négatives. Si les bornes calculées à l'aide des formules sont négatives, elles sont définies sur zéro.
Pour tous les rapports compris entre 0 et 1, les limites inférieure et supérieure doivent également se trouver entre 0 et 1. Les limites se trouvant en dehors de l'étendue sont définies sur 0 ou 1 en conséquence.
Notation
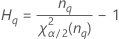
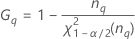
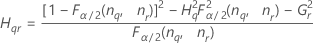
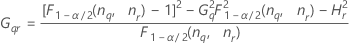
| Terme | Description |
|---|---|
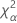 | le percentile α * 100 de la loi du Khi deux avec nq degrés de liberté |
| Fα(nq, nγ) | le percentile α * 100 de la loi F avec nq et nγ degrés de liberté |
| I | nombre de pièces |
| J | nombre d'opérateurs |
| K | nombre de répétitions |
Pour les degrés de liberté :
Pièces : n1=I–1
Opérateurs : n2=J–1
Pièces*Opérateurs: n3= (I–1)(J–1)
Répétitions : n4=IJ(K–1)
CMPièces = S12
CMOpérateur = S22
CMPièce*Opérateur = S32
CMRépétitions = S42
Intervalle de confiance des composantes de la variance de répétabilité
Minitab calcule les bornes inférieure et supérieure d'un intervalle de confiance exact de (1-α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Formules
- Avec opérateur
-

- Sans opérateur
-

- Sans terme d'interaction
-

Notation
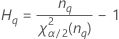
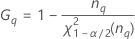
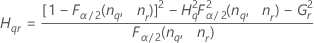
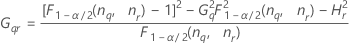
| Terme | Description |
|---|---|
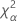 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de la variance de reproductibilité (ou Opérateur)
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Formules
- Avec terme d'interaction
-

- Sans terme d'interaction
-

Notation
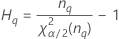
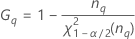
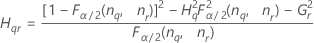
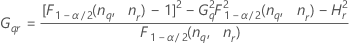
| Terme | Description |
|---|---|
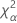 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de la variance du terme Opérateur
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Formules


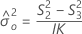
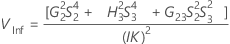
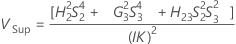
Notation
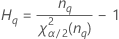
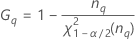
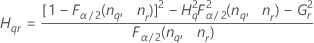
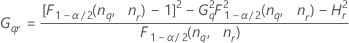
| Terme | Description |
|---|---|
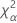 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de la variance d'interaction
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Formules


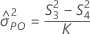

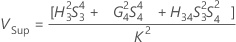
Notation
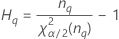
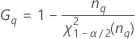
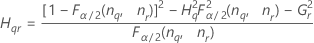
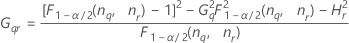
| Terme | Description |
|---|---|
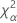 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de la variance de l'instrumentation totale
Avec terme Opérateur et terme d'interaction
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.

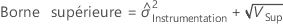
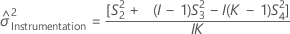
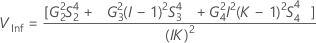
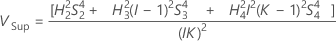
Sans terme Opérateur
Les bornes inférieure et supérieure d'un intervalle de confiance exact de (1-α) *100 % sont les suivantes :


Sans terme d'interaction
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.

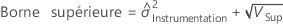

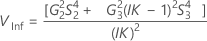
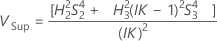
Notation
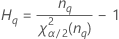
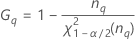
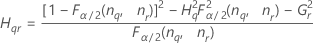
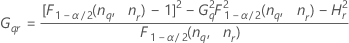
| Terme | Description |
|---|---|
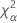 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de variance de pièce à pièce
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G
Avec opérateur




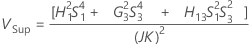
Sans opérateur


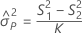
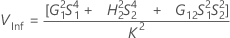

Sans interaction




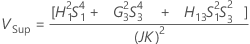
Notation
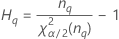
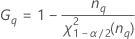
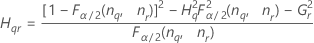
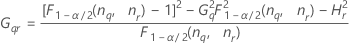
| Terme | Description |
|---|---|
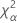 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |
Intervalle de confiance des composantes de la variance totale
Minitab utilise la méthode des grands échantillons modifiés pour calculer les bornes inférieure et supérieure d'un intervalle de confiance approximatif de (1–α) *100 %. Pour calculer les bornes de confiance unilatérales, remplacez α/2 par α dans H et G.
Avec opérateur



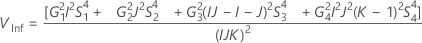
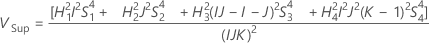
Sans opérateur


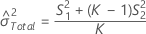
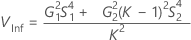
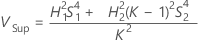
Sans terme d'interaction


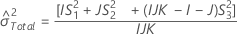
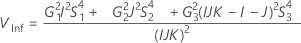
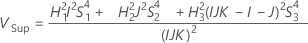
Notation
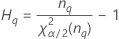
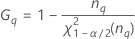
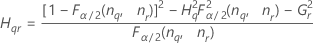
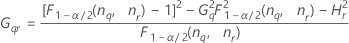
| Terme | Description |
|---|---|
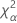 | le α *100e percentile de la loi du Khi deux avec nq degrés de liberté |
| J | nombre d'opérateurs |
| I | nombre de pièces |
| K | nombre de répétitions |