Sur ce thème
Biais
Le biais est une mesure de l'exactitude d'un système de mesure. Le biais est calculé comme la différence entre la valeur du standard connue d'une pièce de référence et la moyenne observée des mesures.
Interprétation
- Un biais positif indique que l'instrumentation surestime.
- Un biais négatif indique que l'instrumentation sous-estime.
Pour une instrumentation qui mesure avec exactitude, le %biais sera petit. Utilisez la valeur de p afin de déterminer si le biais est statistiquement significatif.
Répétabilité et répétabilité pré-ajustée
La répétabilité est la quantité de variation dans le système de mesure due à l'instrumentation. L'étude de l'instrumentation d'attribut effectue une régression des probabilités d'acceptation sur les valeurs de référence pour obtenir la répétabilité.
La répétabilité pré-ajustée est la répétabilité calculée avant l'ajustement pour tenir compte de la surestimation. Minitab divise les estimations de répétabilité par le facteur d'ajustement 1,08 pour calculer la répétabilité ajustée. Le facteur d'ajustement de 1,08 est fourni par l'Automotive Industry Action Group (AIAG)1.
Interprétation
Une valeur de répétabilité basse indique une mesure régulière de l'instrumentation. Une valeur de répétabilité élevée indique une variation aléatoire ou des problèmes tels qu'une sélection inadéquate des pièces ou une mauvaise instrumentation.
Minitab utilise, dans le calcul, la valeur de la répétabilité ajustée pour tester l'hypothèse nulle selon laquelle le biais est nul.
Droite de Henry
La droite de Henry indique le pourcentage d'acceptations pour chaque valeur de référence. Etant donné que l'instrumentation ne comporte pas de mesures réelles permettant d'estimer le biais et la répétabilité, Minitab calcule ces valeurs en ajustant la courbe de distribution normale à l'aide des probabilités d'acceptation calculées et des valeurs de référence connues pour toutes les pièces.
Si les erreurs de mesure suivent une loi normale, les probabilités calculées se situent sur une ligne droite. Une droite de régression est ajustée aux probabilités.
Interprétation
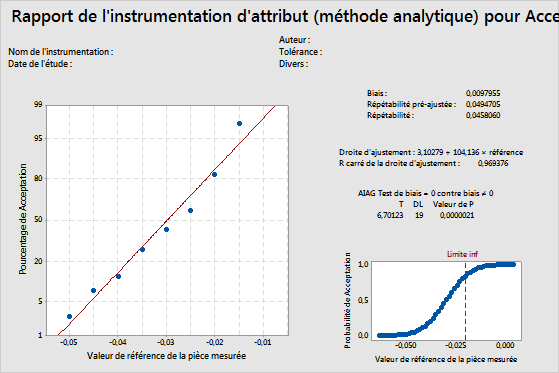
Droite d'ajustement
La probabilité d'acceptation pour chaque pièce est calculée et représentée sur une droite de Henry. Sur une droite de Henry, la valeur y d'un point relevé = Φ–1(Probabilité d'acceptation), Φ–1 correspondant à l'inverse de la fonction de répartition cumulée normale standard.
Une droite de régression ajustée est tracée sur les points relevés.
Interprétation
Si la droite d'ajustement s'ajuste correctement aux points relevés, Minitab utilise les valeurs d'ordonnée à l'origine et de pente pour calculer les valeurs de biais et de répétabilité.

Ce graphique montre que la droite d'ajustement s'ajuste correctement aux données.
R carré de la droite d'ajustement
La valeur R carré (R2) de la droite de régression ajustée indique le pourcentage de variation dans la probabilité des réponses d'acceptation expliquée par le modèle de régression.
Interprétation
R2 est comprise entre 0 et 100 %. En général, plus la valeur R2 est élevée, plus le modèle est ajusté à vos données. Les valeurs R2 qui sont supérieures à 90 % indiquent en général un excellent ajustement des données.

Pour cet exemple, la valeur R carré est de 0,969376. La droite d'ajustement correspond parfaitement aux données et le modèle représente près de 97 % de la variance.
T
T est la statistique t de l'hypothèse alternative selon laquelle le biais est différent de 0.
Le test t compare cette statistique t observée à une valeur critique sur la loi T avec (n-1) degrés de liberté pour déterminer si le biais du système de mesure est statistiquement significatif.
DL
La valeur des degrés de liberté (DL) est utilisée pour déterminer la valeur de p. Pour la méthode AIAG, DL = nombre d'essais – 1. Pour la méthode de régression, la valeur DL = nombre de points utilisés pour créer la droite d'ajustement – 2.
Valeur de p
Pour déterminer si le système de mesure présente un biais statistiquement significatif, comparez la valeur de p au seuil de signification. En général, un seuil de signification (noté alpha ou α) de 0,05 fonctionne bien. Un seuil de signification de 0,05 indique 5 % de risques de conclure à tort que le système présente un biais.
Interprétation
Une valeur de p inférieure fournit des preuves plus solides par rapport à l'hypothèse nulle. Si la valeur de p est inférieure à la valeur α, vous pouvez rejeter l'hypothèse nulle selon laquelle le biais dans le système de mesure est égal à 0.
Courbe des performances de l'instrumentation
La courbe des performances de l'instrumentation présente l'estimation de la probabilité d'acceptation comme fonction de la valeur de référence pour l'élément. La ligne de référence verticale indique les limites saisies pour l'analyse.
Interprétation
Si vous indiquez une limite de tolérance inférieure, les valeurs de référence et les probabilités d'acceptation indiquent une croissance. Si vous indiquez une limite de tolérance supérieure, les probabilités d'acceptation diminuent à mesure que les valeurs de référence augmentent.
Si une instrumentation a une limite supérieure et inférieure et que vous pouvez supposer une linéarité et une uniformité de l'erreur, vous pouvez afficher les limites de tolérance supérieure et inférieure sur la courbe des performances de l'instrumentation. La courbe apparaît sous forme d'image en miroir.
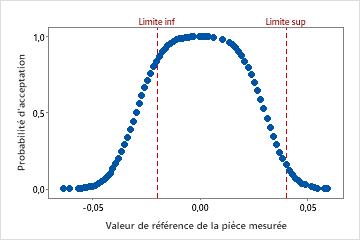
Pour ces données, la probabilité d'accepter un élément à la limite de tolérance inférieure (Limite inf) de –0,020 est élevée. La probabilité d'acceptation augmente au fur et à mesure que les valeurs de référence augmentent jusqu'à la valeur de référence de 0,01. Ensuite, la probabilité d'acceptation décroît. La probabilité d'acceptation à la limite de tolérance supérieure (Limite sup) est d'environ 0,15.
