Sur ce thème
Coefficient de concordance de Kendall
Utilisez la statistique de Kendall avec des données ordinales de trois niveaux minimum.
Dans la description de la méthode, sans perte de généralité, nous supposons qu'une notation unique sur chaque sujet est réalisée par chaque évaluateur et qu'il existe k évaluateurs par sujet. Ensuite, dans le calcul du coefficient de corrélation de Kendall, les k évaluateurs représentent les k essais pour chaque évaluateur.
Supposons que les données soient organisées dans un tableau k x N, chaque ligne représentant les rangs affectés par un évaluateur particulier aux N sujets.
Formules
Lorsque le standard réel n'est pas connu, Minitab estime le coefficient de Kendall par :
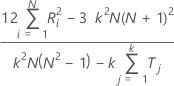
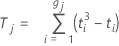
Notation
| Terme | Description |
|---|---|
| N | nombre de sujets |
| Σ Ri2 | somme des sommes carrées de rangs pour chacun des N sujets classés |
| K | nombre d'évaluateurs |
| Tj | Tj affecte la moyenne des notations à l'observation liée |
| Terme | Description |
|---|---|
| ti | nombre de rangs liés dans le ième regroupement de nombres de même grandeur |
| gj | Nombre de regroupements de nombres de même grandeur dans le jème ensemble de rangs |
Test de la signification du coefficient de concordance de Kendall
Pour tester la signification du coefficient de Kendall, utilisez :
c 2= k (N – 1) W
Notation
| Terme | Description |
|---|---|
| c 2 | est distribué sous forme de Khi deux avec N – 1 degrés de liberté |
| k | nombre d'évaluateurs |
| N | nombre de sujets |
| W | coefficient de Kendall calculé |
Coefficient de corrélation de Kendall
Utilisez la statistique de Kendall avec des données ordinales de trois niveaux minimum.
Dans la description de la méthode, sans perte de généralité, nous supposons qu'une notation unique sur chaque sujet est réalisée par chaque évaluateur et qu'il existe k évaluateurs par sujet. Ensuite, dans le calcul du coefficient de corrélation de Kendall, les k évaluateurs représentent les k essais effectués par tous les évaluateurs.
Lorsque le standard est connu, Minitab estime le coefficient de corrélation de Kendall en calculant la moyenne des coefficients de Kendall entre chaque évaluateur et le standard.
Le coefficient de corrélation de Kendall pour la concordance des essais avec le standard connu est la moyenne des coefficients de corrélation de Kendall, d'un essai à l'autre.
Formules
Minitab calcule le coefficient de Kendall entre chaque essai et le standard à l'aide des formules suivantes :

Notation
| Terme | Description |
|---|---|
| TX | nombre de paires liées sur X = 0,5 Σi ni+ (ni+– 1) |
| TY | nombre de paires liées sur Y = 0,5 Σj n+j (n+j– 1) |
| C | nombre de paires concordantes = Σi<kΣj<l nij nkl |
| D | nombre de paires discordantes = Σi<kΣj>l nij nkl |
| Terme | Description |
|---|---|
| ni+ | nombre d'observations dans la ième ligne |
| n+j | nombre d'observations dans la jème colonne |
| nij | observations dans la cellule correspondant à la ième ligne et à la jème colonne |
| nkl | observations dans la cellule correspondant à la kème et à la lème colonne |
| n++ | nombre total d'observations |
Références
A. Agresti (1984). Analysis of Ordinal Categorical Data, John Wiley & Sons.
Test de la signification du coefficient de corrélation de Kendall
Formule
Pour tester la signification du coefficient de Kendall lorsque le standard réel est connu, utilisez :
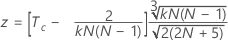
utilisez :
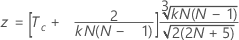
Notation
| Terme | Description |
|---|---|
| Tc | moyenne des coefficients de corrélation de Kendall entre chaque évaluateur et le standard |
| N | nombre total de sujets |
| k | nombre d'évaluateurs |
