Méthodes et formules des statistiques kappa pour Analyse de concordance

Sélectionnez la méthode ou la formule de votre choix.

Sur ce thème

Statistique kappa de Cohen (standard inconnu)
Statistique kappa de Cohen (standard connu)
Test de la signification du kappa de Cohen
Statistique kappa de Fleiss (standard inconnu)
Test de la signification du kappa de Fleiss (standard connu)
Statistique kappa de Fleiss (standard connu)
Test de la signification du kappa de Fleiss (standard connu)

Statistique kappa de Cohen (standard inconnu)

Utilisez la statistique kappa de Cohen lorsque les classifications sont nominales. Lorsque le standard est inconnu et que vous choisissez d'obtenir le kappa de Cohen, Minitab calcule la statistique lorsque les données répondent aux conditions suivantes :

Intra-évaluateur : il existe exactement deux essais avec un évaluateur
Inter-évaluateurs : il existe exactement deux évaluateurs ayant chacun un seul essai

Pour une valeur de réponse particulière, il est possible de calculer le kappa en réduisant toutes les réponses qui ne sont pas égales à la valeur dans une catégorie. Vous pouvez ensuite utiliser le tableau 2 x 2 pour calculer le kappa.

Formules

Lorsque le standard réel n'est pas connu, Minitab estime le kappa de Cohen par :

	Essai B (ou Evaluateur B)
Essai A (ou Evaluateur A)	1	2	...	k	Total
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Total	p_.+1	p_.+2	...	p_.+k	1

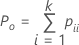
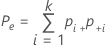
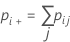
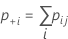
Notation

Terme	Description
P_o	proportion observée de concordance
p_ii	chaque valeur de la diagonale du tableau à deux entrées
P_e	proportion de concordance attendue entre k évaluateurs
n_ij	nombre d'échantillons dans la i^ème ligne et la j^ème colonne
N	nombre total d'échantillons

Statistique kappa de Cohen (standard connu)

Utilisez la statistique kappa de Cohen lorsque les classifications sont nominales. Lorsque le standard est connu et que vous choisissez d'obtenir le kappa de Cohen, Minitab calcule la statistique à l'aide des formules suivantes :

Le coefficient de kappa pour la concordance des essais avec le standard connu est la moyenne de ces coefficients de kappa.

Formules

Lorsque le standard réel est connu, commencez par calculer le kappa à l'aide des données de chaque essai et du standard connu.

	Standard
Essai A	1	2	...	k	Total
1	p₁₁	p₁₂	...	p_1k	p₁₊
2	p₂₁	p₂₂	...	p_2k	P₂₊
....
k	p_k1	p_k2	...	p_kk	p_k+.
Total	p_.+1	p_.+2	...	p_.+k	1

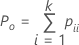
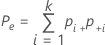
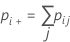
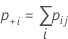
Notation

Terme	Description
P_o	proportion observée de concordance
p_ii	chaque valeur de la diagonale du tableau à deux entrées
P_e	proportion de concordance attendue entre k évaluateurs
n_ij	nombre d'échantillons dans la i^ème ligne et la j^ème colonne
N	nombre total d'échantillons

Test de la signification du kappa de Cohen

Pour tester l'hypothèse nulle selon laquelle les notations sont indépendantes (de façon à ce que kappa = 0), utilisez :

z = kappa / ErT du kappa

Il s'agit d'un test unilatéral. Dans le cadre de l'hypothèse nulle, z suit la loi normale standard. Rejetez l'hypothèse si la valeur z est largement supérieure à la valeur critique d'α.

Formules

L'erreur type du kappa pour chaque essai et le standard est :

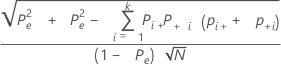
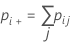
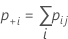
Notation

Terme	Description
P_e	proportion de concordance attendue entre k évaluateurs
N	nombre total d'échantillons

Statistique kappa de Fleiss (standard inconnu)

Deux cas peuvent se présenter pour le calcul des statistiques kappa.

Cas 1 — Concordance intra-évaluateur: Calculez les coefficients de kappa qui représentent la concordance intra-évaluateur.; Dans ce cas, m = nombre d'essais intra-évaluateur, m est supposé >1. L'analyste souhaite examiner la concordance entre les m essais intra-évaluateur. Nous supposons ici que chaque essai est réalisé dans le cas où l'évaluateur ne se souvient pas des notations des essais précédents.
Cas 2 — Concordance entre tous les évaluateurs: Calculez les coefficients de kappa qui représentent la concordance entre tous les évaluateurs.; Dans ce cas, m = nombre total d'essais pour tous les évaluateurs. Le nombre d'évaluateurs est supposé être supérieur à 1, le nombre d'essais peut être égal ou supérieur à 1. L'analyste s'intéresse à la concordance entre tous les évaluateurs.

Formules pour le kappa global

Définissez x_ij sur le nombre de notations sur l'échantillon i dans la catégorie j, i étant compris entre 1 et n, et j étant compris entre 1 et k.

Le coefficient de kappa global est défini par :

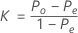
où :

P_o est la proportion observée de la concordance deux à deux parmi les m essais.

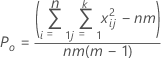
P_e est la proportion de concordance attendue si les notations d'un essai ne sont pas dépendantes.

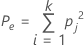
p_j représente la proportion globale de notations dans la catégorie j.

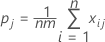
Si l'on substitue P_o et P_e par K, le coefficient de kappa global est estimé par :

où :

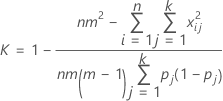
Terme	Description
k	nombre total de catégories
m	nombre d'essais : pour le cas 1, m = nombre d'essais pour chaque évaluateur ; pour le cas 2, m = nombre d'essais pour tous les évaluateurs.
n	nombre d'échantillons
x_ij	nombre de notations sur l'échantillon i dans la catégorie j

Formules pour le kappa pour une catégorie unique

Pour mesurer la concordance par rapport aux classifications dans une seule des k catégories, soit la j^ème, il est possible de combiner toutes les catégories, autres que celle qui nous intéresse, en une seule catégorie et d'appliquer l'équation ci-dessus. La formule obtenue pour la statistique kappa pour la j^ème catégorie est :

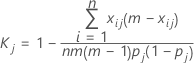
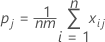
où :

Terme	Description
k	nombre total de catégories
m	nombre d'essais : pour le cas 1, m = nombre d'essais pour chaque évaluateur ; pour le cas 2, m = nombre d'essais pour tous les évaluateurs.
n	nombre d'échantillons
x_ij	nombre de notations sur l'échantillon i dans la catégorie j

Test de la signification du kappa de Fleiss (standard connu)

L'hypothèse nulle, H₀, est la suivante : kappa = 0. L'hypothèse alternative, H₁, est la suivante : > 0.

Dans le cadre de l'hypothèse nulle, Z est distribué à peu près normalement et est utilisé pour calculer les valeurs de p.

Formules

Pour tester si kappa > 0, utilisez la statistique Z suivante :

Var (K) est calculé par :

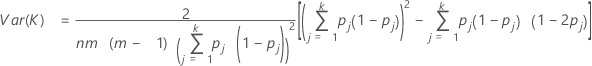
Pour tester si le kappa > 0 pour la j^ème catégorie, utilisez la statistique Z suivante :

Var (K_j) est calculé par :

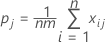
Notation

Terme	Description
K	statistique kappa globale
K_j	statistique kappa pour la j^ème catégorie
k	nombre total de catégories
m	nombre d'essais pour le cas 1, m = nombre d'essais pour chaque évaluateur ; pour le cas 2, m = nombre d'essais pour tous les évaluateurs.
n	nombre d'échantillons
x_ij	nombre de notations sur l'échantillon i dans la catégorie j

Statistique kappa de Fleiss (standard connu)

Suivez les étapes ci-dessous pour calculer le kappa global et le kappa relatif à une catégorie spécifique lorsque la notation standard pour chaque échantillon est connue.

Supposons qu'il existe m essais.

Remarque

Voir les formules de la statistique kappa de Fleiss (standard inconnu).

Pour chaque essai, calculez le kappa à l'aide des notations issues de l'essai et des notations données par le standard. En d'autres termes, considérez le standard comme un autre essai, et utilisez les formules du kappa du standard inconnu pour deux essais pour estimer le kappa.
Répétez le calcul pour les m essais.
Vous disposez maintenant de m valeurs de kappa global et de m valeurs de kappa pour les valeurs de catégorie spécifiques.

Le kappa global avec un standard connu est ensuite égal à la moyenne des m valeurs du kappa global.

De même, le kappa relatif à une catégorie spécifique avec un standard connu est égal à la moyenne des m valeurs de kappa pour une catégorie spécifique.

Test de la signification du kappa de Fleiss (standard connu)

L'hypothèse nulle, H₀, est la suivante : kappa = 0. L'hypothèse alternative, H₁, est la suivante : kappa > 0.

Dans le cadre de l'hypothèse nulle, Z est distribué à peu près normalement et est utilisé pour calculer les valeurs de p.

K correspond à la statistique kappa, et Var(K) à la variance de la statistique kappa.

Remarque

Voir les formules de la statistique kappa de Fleiss (standard inconnu)

Supposons qu'il existe m essais.

Pour chaque essai, calculez la variance du kappa à l'aide des notations de l'essai, et des notations données par le standard. En d'autres termes, considérez le standard comme le second essai, et utilisez la variance des formules du kappa pour deux cas d'essai et de standard inconnu pour calculer la variance.
Répétez le calcul pour les m essais.
Vous disposez maintenant de m variances pour le kappa global et de m variances pour le kappa pour des catégories spécifiques.

La variance du kappa global avec des standards connus est ensuite égale à la somme des m variances pour le kappa global divisée par m².

De même, la variance du kappa pour une catégorie spécifique avec un standard connu est égale à la somme des m variances pour le kappa pour une catégorie spécifique divisée par m².