Si vos données présentent une surdispersion ou une sous-dispersion, l'utilisation d'une carte aux attributs de Laney (Carte P′ de Laney ou Carte U′ de Laney) peut vous permettre de distinguer la variation due aux causes communes et la variation due aux causes spéciales de manière plus exacte qu'une carte aux attributs traditionnelle (par exemple, Carte P ou Carte U). Les calculs des cartes aux attributs de Laney incluent Sigma Z, qui est un ajustement pour la surdispersion ou la sous-dispersion. Une valeur de Sigma Z de 1 indique qu'aucun ajustement n'est nécessaire et que la carte aux attributs de Laney est exactement la même que la carte aux attributs traditionnelle.
Pour créer une carte P' de Laney, sélectionnez . Pour créer une carte U' de Laney, sélectionnez .
Qu'est-ce que la surdispersion ?
Il existe une surdispersion lorsque les données présentent plus de variation que prévu en se basant sur une loi binomiale (pour les défectueux) ou sur une loi de Poisson (pour les défauts). Les cartes P et U traditionnelles supposent que votre taux de défectueux ou de défauts reste constant dans le temps. Cependant, des facteurs de bruit externes, qui ne sont pas des causes spéciales, engendrent habituellement une certaine variation du taux de défectueux ou de défauts dans le temps.
Les limites de contrôle d'une carte P ou U traditionnelle deviennent plus étroites lorsque vos sous-groupes sont plus grands. Si vos sous-groupes sont suffisamment grands, la surdispersion peut avoir pour conséquence que les points semblent hors contrôle alors qu'ils ne le sont pas. Pour la carte aux attributs de Laney, la définition d'une variation due à des causes communes n'inclut pas seulement la variation à l'intérieur des sous-groupes, mais également la variation moyenne entre les sous-groupes consécutifs. En cas de surdispersion, les limites de contrôles d'une carte aux attributs de Laney sont plus larges que celles d'une carte aux attributs traditionnelle.
La relation entre l'effectif de l'échantillon et les limites de contrôle sur une carte de contrôle aux attributs traditionnelle est semblable à celle existant entre la puissance et le test t à 1 échantillon. Plus les échantillons sont grands, plus le test t est puissant et permet de détecter une différence. Toutefois, si l'échantillon est suffisamment grand, même une très petite différence non digne d'intérêt peut devenir significative. Par exemple, avec un échantillon de 1 000 000 observations, un test t peut déterminer qu'un échantillon moyen de 50,001 est significativement différent de 50. Pourtant, une différence de 0,001 peut ne pas avoir de conséquences pratiques sur votre procédé.
Qu'est-ce que la sous-dispersion ?
La sous-dispersion est l'opposé de la surdispersion. Il existe une sous-dispersion lorsque les données présentent moins de variation que prévu en se basant sur une loi binomiale (pour les défectueux) ou sur une loi de Poisson (pour les défauts). La surdispersion peut se produire lorsque des sous-groupes adjacents sont corrélés les uns avec les autres. On appelle également ce processus l'autocorrélation.
Lorsque les données affichent une sous-dispersion, les limites de contrôle d'une carte P ou une carte U traditionnelle peuvent être trop larges. Si les limites de contrôle sont trop larges, vous pouvez négliger une variation due aux causes spéciales et la prendre pour une variation due aux causes communes. En cas de sous-dispersion, les limites de contrôles d'une carte aux attributs de Laney sont plus étroites que celles d'une carte aux attributs traditionnelle.
Par exemple, à mesure qu'un outil s'use, le nombre de défauts peut s'accroître. L'augmentation du nombre de défauts dans les sous-groupes peut les rendre plus semblables qu'ils ne le seraient par hasard.
Comparaison de cartes aux attributs traditionnelles aux cartes aux attributs de Laney
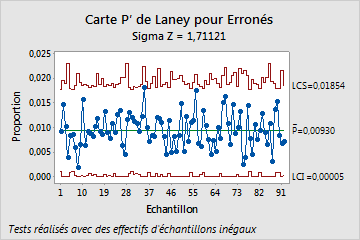
Les graphiques suivants présentent une carte P classique et une carte P' de Laney portant sur les mêmes données. Ces données sont également représentées dans l'exemple de la carte P' de Laney et l'exemple de la carte de diagnostic P. Les sous-groupes sont très grands, comptant chacun 2 500 observations en moyenne. Par ailleurs, le test de la carte de diagnostic P indique une surdispersion dans les données.
Sur la carte P tradtionnelle, les grands effectifs de sous-groupes entraînent des limites de contrôle très étroites. Avec l'étroitesse des limites de contrôle, plusieurs sous-groupes apparaissent hors contrôle en raison de la surdispersion. Touterfois, la carte P' de Laney corrige la surdispersion et montre que le procédé est en réalité maîtrisé. Aucun point ne se situe à l'extérieur des limites de contrôle.
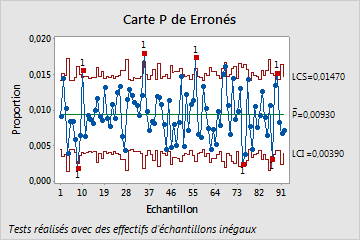
Carte P classique