Sigma (σ) est l'écart type du procédé. Si vous entrez une valeur historique pour σ, Minitab utilise cette valeur historique. Sinon, Minitab utilise une des méthodes suivantes pour estimer σ à partir des données.
Sur ce thème
Méthode R barre
Minitab utilise l'étendue de chaque sous-groupe,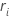 
, pour calculer 
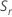, qui est un estimateur non biaisé de σ :
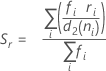
où
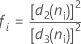
Lorsque l'effectif de sous-groupe est constant, la formule peut être simplifiée comme suit :
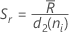
où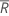 
(R barre) est la moyenne des étendues des sous-groupes, calculée comme suit :
Notation
| Terme | Description |
|---|---|
| ri | étendue pour le sous-groupe i |
| m | nombre de sous-groupes |
| d2(·) | valeur de la constante de correction de biais d2 correspondant à la valeur indiquée entre parenthèses |
| ni | nombre d'observations dans le sous-groupe i |
| d3(·) | valeur de la constante de correction de biais d3 correspondant à la valeur indiquée entre parenthèses |
Méthode de l'écart type regroupé
L'écart type regroupé (Sp) est obtenu avec la formule suivante :
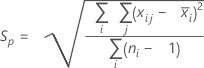
Lorsque l'effectif de sous-groupe est constant, Sp peut également être calculé comme suit :
Avec constante de correction de biais
Par défaut, Minitab applique la constante de correction de biais, c4(), lorsque vous utilisez l'écart type regroupé pour estimer σ :
Notation
| Terme | Description |
|---|---|
| xij | je observation du ie sous-groupe |
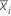 | moyenne du sous-groupe i |
| ni | nombre d'observations dans le sous-groupe i |
| μv | moyenne des variances de sous-groupes |
| c4(·) | valeur de la constante de correction de biais c4 correspondant à la valeur spécifiée entre parenthèses |
| j | degrés de liberté pour Sp, obtenus avec la formule suivante :
 |
