L'écart type du procédé est également appelé sigma, ou σ. Si vous entrez une valeur historique pour sigma, Minitab utilise cette valeur historique. Sinon, Minitab utilise une des méthodes suivantes pour estimer sigma à partir des données.
Sur ce thème
Méthode R barre
Minitab utilise l'étendue de chaque sous-groupe, 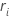 , pour calculer
, pour calculer 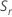 , qui est un estimateur non biaisé de σ :
, qui est un estimateur non biaisé de σ :
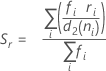
où
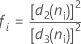
Lorsque l'effectif de sous-groupe est constant, la formule peut être simplifiée comme suit :
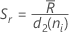
où 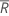 (R barre) est la moyenne des étendues des sous-groupes, calculée comme suit :
(R barre) est la moyenne des étendues des sous-groupes, calculée comme suit :

Notation
| Terme | Description |
|---|---|
| ri | étendue pour le sous-groupe i |
| m | nombre de sous-groupes |
| d2(·) | valeur de la constante de correction de biais d2 correspondant à la valeur indiquée entre parenthèses |
| ni | nombre d'observations dans le sous-groupe i |
| d3(·) | valeur de la constante de correction de biais d3 correspondant à la valeur indiquée entre parenthèses |
Méthode de l'écart type regroupé
L'écart type regroupé (Sp) est obtenu avec la formule suivante :
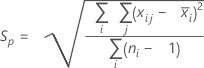
Lorsque l'effectif de sous-groupe est constant, Sp peut également être calculé comme suit :

Avec constante de correction de biais
Par défaut, Minitab applique la constante de correction de biais, c4(), lorsque vous utilisez l'écart type regroupé pour estimer σ :


Notation
| Terme | Description |
|---|---|
| xij | je observation du ie sous-groupe |
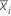 | moyenne du sous-groupe i |
| ni | nombre d'observations dans le sous-groupe i |
| μv | moyenne des variances de sous-groupes |
| c4(·) | valeur de la constante de correction de biais c4 correspondant à la valeur spécifiée entre parenthèses |
| j | degrés de liberté pour Sp, obtenus avec la formule suivante :
 |
Constantes de correction de biais d2(), d3() et d4()
d2(N) représente la valeur attendue pour l'étendue de N observations dans une population normale avec un écart type de 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors E(r) = d2(N)σ.
d3(N) représente l'écart type de l'étendue de N observations dans une population normale avec σ = 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors Ecart type(r) = d3(N)σ.
Utilisez le tableau suivant pour obtenir la constante de correction de biais pour une valeur donnée, N. (Pour déterminer la valeur de N, consultez la formule de la statistique correspondante.)

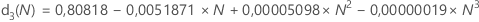
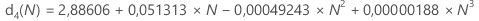
- D. J. Wheeler et D. S. Chambers (1992), Understanding Statistical Process Control, seconde édition, SPC Press, Inc.
- H. Leon Harter (1960), "Tables of Range and Studentized Range", The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1,128 | 0,8525 | 0,954 |
| 3 | 1,693 | 0,8884 | 1,588 |
| 4 | 2,059 | 0,8798 | 1,978 |
| 5 | 2,326 | 0,8641 | 2,257 |
| 6 | 2,534 | 0,848 | 2,472 |
| 7 | 2,704 | 0,8332 | 2,645 |
| 8 | 2,847 | 0,8198 | 2,791 |
| 9 | 2,97 | 0,8078 | 2,915 |
| 10 | 3,078 | 0,7971 | 3,024 |
| 11 | 3,173 | 0,7873 | 3,121 |
| 12 | 3,258 | 0,7785 | 3,207 |
| 13 | 3,336 | 0,7704 | 3,285 |
| 14 | 3,407 | 0,763 | 3,356 |
| 15 | 3,472 | 0,7562 | 3,422 |
| 16 | 3,532 | 0,7499 | 3,482 |
| 17 | 3,588 | 0,7441 | 3,538 |
| 18 | 3,64 | 0,7386 | 3,591 |
| 19 | 3,689 | 0,7335 | 3,64 |
| 20 | 3,735 | 0,7287 | 3,686 |
| 21 | 3,778 | 0,7242 | 3,73 |
| 22 | 3,819 | 0,7199 | 3,771 |
| 23 | 3,858 | 0,7159 | 3,811 |
| 24 | 3,895 | 0,7121 | 3,847 |
| 25 | 3,931 | 0,7084 | 3,883 |
| N | d2(N) |
|---|---|
| 26 | 3,964 |
| 27 | 3,997 |
| 28 | 4,027 |
| 29 | 4,057 |
| 30 | 4,086 |
| 31 | 4,113 |
| 32 | 4,139 |
| 33 | 4,165 |
| 34 | 4,189 |
| 35 | 4,213 |
| 36 | 4,236 |
| 37 | 4,259 |
| 38 | 4,28 |
| 39 | 4,301 |
| 40 | 4,322 |
| 41 | 4,341 |
| 42 | 4,361 |
| 43 | 4,379 |
| 44 | 4,398 |
| 45 | 4,415 |
| 46 | 4,433 |
| 47 | 4,45 |
| 48 | 4,466 |
| 49 | 4,482 |
| 50 | 4,498 |
Constantes de correction de biais c4() et c5()
c4()

c5()

Notation
| Terme | Description |
|---|---|
| Γ() | Fonction gamma |
