Méthodes et formules pour la fonction Cartes de contrôle des individus

Points relevés

Chaque point de données, x_i, est une observation.

Ligne centrale

La ligne centrale représente la moyenne du procédé, μ. Si vous ne spécifiez pas de valeur historique pour la moyenne du procédé, Minitab utilise la moyenne des observations.

Limites de contrôle

Si vous ne spécifiez pas de valeur historique pour l'écart type du procédé, σ, Minitab détermine σ à partir de vos données en utilisant la méthode indiquée.

Limite de contrôle inférieure (LCI)

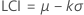
Limite de contrôle supérieure (LCS)

Notation

Terme	Description
μ	moyenne du procédé
k	paramètre pour le test 1 (la valeur par défaut est 3)

Méthode de la moyenne de l'étendue mobile

La moyenne de l'étendue mobile, , de longueur w est obtenue par la formule suivante :

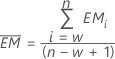
où EM_i est l'étendue mobile pour l'observation i, calculée comme suit :

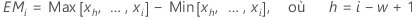
Minitab utilise pour calculer S_em, qui est une estimation non biaisée de σ :

Notation

Terme	Description
n	nombre d'observations
w	longueur de l'étendue mobile. La valeur par défaut est 2.
d₂()	valeur de la constante de correction de biais d₂ correspondant à la valeur indiquée entre parenthèses

Estimations de Nelson

Utilisez les estimations de Nelson pour corriger toute valeur d'étendue mobile anormalement élevée dans le calcul des limites de contrôle. La procédure est similaire à celle proposée par Nelson¹ Minitab élimine toute valeur d'étendue mobile supérieure de plus de 3 σ à l'étendue mobile moyenne, puis recalcule cette dernière et les limites de contrôle.

Méthode de la médiane de l'étendue mobile

La médiane de l'étendue mobile, , de longueur w est obtenue par la formule suivante :

où EM_i est l'étendue mobile pour l'observation i, calculée comme suit :

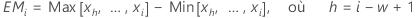
Minitab utilise pour calculer S_em, qui est une estimation non biaisée de σ :

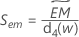
Notation

Terme	Description
n	nombre d'observations
w	longueur de l'étendue mobile. La valeur par défaut est 2.
d₄()	valeur de la constante de correction de biais d₄ correspondant à la valeur indiquée entre parenthèses

Méthode pour la racine carrée de MSSD

MSSD (pour Mean of squared successive differences) est la moyenne des différences successives carrées. La racine carrée de MSSD (SRMSSD) est calculée de la manière suivante :

Avec constante de correction de biais

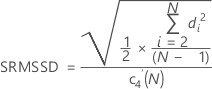
Sans constante de correction de biais

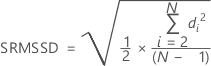
Notation

Terme	Description
d_i	différence entre la valeur de l'observation i et celle de l'observation i – 1
N	nombre d'observations
c₄'(N)	constante de correction de biais issue d'un tableau

Constantes de correction de biais d2(), d3() et d4()

d₂(N) représente la valeur attendue pour l'étendue de N observations dans une population normale avec un écart type de 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors E(r) = d₂(N)σ.

d₃(N) représente l'écart type de l'étendue de N observations dans une population normale avec σ = 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors Ecart type(r) = d₃(N)σ.

Utilisez le tableau suivant pour obtenir la constante de correction de biais pour une valeur donnée, N. (Pour déterminer la valeur de N, consultez la formule de la statistique correspondante.)

Pour les valeurs de N comprises entre 51 et 100, utilisez l'approximation suivante pour d₂(N) :

Pour les valeurs de N comprises entre 26 et 100, utilisez l'approximation suivante pour d₃(N) et d₄(N) :

Pour plus d'informations sur ces constantes, consultez les ouvrages suivants :

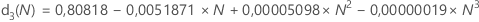
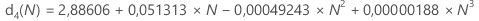
D. J. Wheeler et D. S. Chambers (1992), Understanding Statistical Process Control, seconde édition, SPC Press, Inc.
H. Leon Harter (1960), "Tables of Range and Studentized Range", The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.

Tableau 1. Tableau de valeurs
N	d₂(N)	d₃(N)	d₄(N)
2	1,128	0,8525	0,954
3	1,693	0,8884	1,588
4	2,059	0,8798	1,978
5	2,326	0,8641	2,257
6	2,534	0,848	2,472
7	2,704	0,8332	2,645
8	2,847	0,8198	2,791
9	2,97	0,8078	2,915
10	3,078	0,7971	3,024
11	3,173	0,7873	3,121
12	3,258	0,7785	3,207
13	3,336	0,7704	3,285
14	3,407	0,763	3,356
15	3,472	0,7562	3,422
16	3,532	0,7499	3,482
17	3,588	0,7441	3,538
18	3,64	0,7386	3,591
19	3,689	0,7335	3,64
20	3,735	0,7287	3,686
21	3,778	0,7242	3,73
22	3,819	0,7199	3,771
23	3,858	0,7159	3,811
24	3,895	0,7121	3,847
25	3,931	0,7084	3,883

N	d₂(N)
26	3,964
27	3,997
28	4,027
29	4,057
30	4,086
31	4,113
32	4,139
33	4,165
34	4,189
35	4,213
36	4,236
37	4,259
38	4,28
39	4,301
40	4,322
41	4,341
42	4,361
43	4,379
44	4,398
45	4,415
46	4,433
47	4,45
48	4,466
49	4,482
50	4,498

Constante de correction de biais c4'()

Utilisez les tableaux suivants pour obtenir les valeurs de la onstante de correction de biais, c₄'(), qui est utilisée dans les formules de la méthode d'estimation sigma appelée racine carrée de MSSD.

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
2	0,79785	41	0,990797	80	0,995215
3	0,87153	42	0,991013	81	0,995272
4	0,905763	43	0,991218	82	0,995328
5	0,925222	44	0,991415	83	0,995383
6	0,937892	45	0,991602	84	0,995436
7	0,946837	46	0,991782	85	0,995489
8	0,953503	47	0,991953	86	0,995539
9	0,958669	48	0,992118	87	0,995589
10	0,962793	49	0,992276	88	0,995638
11	0,966163	50	0,992427	89	0,995685
12	0,968968	51	0,992573	90	0,995732
13	0,971341	52	0,992713	91	0,995777
14	0,973375	53	0,992848	92	0,995822
15	0,975137	54	0,992978	93	0,995865
16	0,976679	55	0,993103	94	0,995908
17	0,978039	56	0,993224	95	0,995949
18	0,979249	57	0,99334	96	0,99599
19	0,980331	58	0,993452	97	0,996030
20	0,981305	59	0,993561	98	0,996069
21	0,982187	60	0,993666	99	0,996108
22	0,982988	61	0,993767	100	0,996145
23	0,98372	62	0,993866	101	0,996182
24	0,984391	63	0,993961	102	0,996218
25	0,985009	64	0,994053	103	0,996253
26	0,985579	65	0,994142	104	0,996288
27	0,986107	66	0,994229	105	0,996322
28	0,986597	67	0,994313	106	0,996356
29	0,987054	68	0,994395	107	0,996389
30	0,98748	69	0,994474	108	0,996421
31	0,987878	70	0,994551	109	0,996452
32	0,988252	71	0,994626	110	0,996483
33	0,988603	72	0,994699	111	0,996514
34	0,988934	73	0,994769	112	0,996544
35	0,989246	74	0,994838	113	0,996573
36	0,98954	75	0,994905	114	0,996602
37	0,989819	76	0,99497	115	0,996631
38	0,990083	77	0,995034	116	0,996658
39	0,990333	78	0,995096	117	0,996686
40	0,990571	79	0,995156	118	0,996713

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
119	0,996739	160	0,997541	201	0,998016
120	0,996765	161	0,997555	202	0,998025
121	0,996791	162	0,99757	203	0,998034
122	0,996816	163	0,997584	204	0,998043
123	0,996841	164	0,997598	205	0,998052
124	0,996865	165	0,997612	206	0,998061
125	0,996889	166	0,997625	207	0,998070
126	0,996913	167	0,997639	208	0,998078
127	0,996936	168	0,997652	209	0,998087
128	0,996959	169	0,997665	210	0,998095
129	0,996982	170	0,997678	211	0,998104
130	0,997004	171	0,997691	212	0,998112
131	0,997026	172	0,997703	213	0,99812
132	0,997047	173	0,997716	214	0,998128
133	0,997069	174	0,997728	215	0,998137
134	0,997089	175	0,997741	216	0,998145
135	0,99711	176	0,997753	217	0,998152
136	0,99713	177	0,997765	218	0,99816
137	0,99715	178	0,997776	219	0,998168
138	0,99717	179	0,997788	220	0,998176
139	0,997189	180	0,9978	221	0,998184
140	0,997209	181	0,997811	222	0,998191
141	0,997227	182	0,997822	223	0,998199
142	0,997246	183	0,997834	224	0,998206
143	0,997264	184	0,997845	225	0,998214
144	0,997282	185	0,997856	226	0,998221
145	0,9973	186	0,997866	227	0,998228
146	0,997318	187	0,997877	228	0,998235
147	0,997335	188	0,997888	229	0,998242
148	0,997352	189	0,997898	230	0,99825
149	0,997369	190	0,997909	231	0,998257
150	0,997386	191	0,997919	232	0,998263
151	0,997402	192	0,997929	233	0,99827
152	0,997419	193	0,997939	234	0,998277
153	0,997435	194	0,997949	235	0,998284
154	0,99745	195	0,997959	236	0,998291
155	0,997466	196	0,997969	237	0,998297
156	0,997481	197	0,997978	238	0,998304
157	0,997497	198	0,997988	239	0,998311
158	0,997512	199	0,997997	240	0,998317
159	0,997526	200	0,998007	241	0,998323

N	c₄'(N)	N	c₄'(N)	N	c₄'(N)
242	0,99833	283	0,998553	324	0,99872
243	0,998336	284	0,998558	325	0,998723
244	0,998342	285	0,998562	326	0,998727
245	0,998349	286	0,998567	327	0,99873
246	0,998355	287	0,998571	328	0,998734
247	0,998361	288	0,998576	329	0,998737
248	0,998367	289	0,99858	330	0,99874
249	0,998373	290	0,998585	331	0,998744
250	0,998379	291	0,998589	332	0,998747
251	0,998385	292	0,998593	333	0,998751
252	0,998391	293	0,998598	334	0,998754
253	0,998397	294	0,998602	335	0,998757
254	0,998403	295	0,998606	336	0,998761
255	0,998408	296	0,998611	337	0,998764
256	0,998414	297	0,998615	338	0,998767
257	0,99842	298	0,998619	339	0,99877
258	0,998425	299	0,998623	340	0,998774
259	0,998431	300	0,998627	341	0,998777
260	0,998436	301	0,998632	342	0,99878
261	0,998442	302	0,998636	343	0,998783
262	0,998447	303	0,99864	344	0,998786
263	0,998453	304	0,998644	345	0,99879
264	0,998458	305	0,998648	346	0,998793
265	0,998463	306	0,998652	347	0,998796
266	0,998469	307	0,998656	348	0,998799
267	0,998474	308	0,99866	349	0,998802
268	0,998479	309	0,998664	350	0,998805
269	0,998484	310	0,998668	351	0,998808
270	0,998489	311	0,998671	352	0,998811
271	0,998495	312	0,998675	353	0,998814
272	0,9985	313	0,998679	354	0,998817
273	0,998505	314	0,998683	355	0,99882
274	0,99851	315	0,998687	356	0,998823
275	0,998515	316	0,99869	357	0,998826
276	0,998519	317	0,998694	358	0,998829
277	0,998524	318	0,998698	359	0,998832
278	0,998529	319	0,998701	360	0,998835
279	0,998534	320	0,998705	361	0,998837
280	0,998539	321	0,998709	362	0,99884
281	0,998544	322	0,998712	363	0,998843
282	0,998548	323	0,998716	364	0,998846

k	c₄'(k)	k	c₄'(k)	k	c₄'(k)
365	0,998849	411	0,998963	457	0,999054
366	0,998851	412	0,998965	458	0,999056
367	0,998854	413	0,998967	459	0,999058
368	0,998857	414	0,99897	460	0,999060
369	0,99886	415	0,998972	461	0,999061
370	0,998862	416	0,998974	462	0,999063
371	0,998865	417	0,998976	463	0,999065
372	0,998868	418	0,998978	464	0,999067
373	0,998871	419	0,99898	465	0,999068
374	0,998873	420	0,998982	466	0,999070
375	0,998876	421	0,998985	467	0,999072
376	0,998879	422	0,998987	468	0,999073
377	0,998881	423	0,998989	469	0,999075
378	0,998884	424	0,998991	470	0,999077
379	0,998886	425	0,998993	471	0,999078
380	0,998889	426	0,998995	472	0,999080
381	0,998892	427	0,998997	473	0,999082
382	0,998894	428	0,998999	474	0,999084
383	0,998897	429	0,999001	475	0,999085
384	0,998899	430	0,999003	476	0,999087
385	0,998902	431	0,999005	477	0,999088
386	0,998904	432	0,999007	478	0,999090
387	0,998907	433	0,999009	479	0,999092
388	0,998909	434	0,999011	480	0,999093
389	0,998912	435	0,999013	481	0,999095
390	0,998914	436	0,999015	482	0,999097
391	0,998917	437	0,999017	483	0,999098
392	0,998919	438	0,999019	484	0,9991
393	0,998921	439	0,999021	485	0,999101
394	0,998924	440	0,999023	486	0,999103
395	0,998926	441	0,999025	487	0,999104
396	0,998929	442	0,999027	488	0,999106
397	0,998931	443	0,999028	489	0,999108
398	0,998933	444	0,999030	490	0,999109
399	0,998936	445	0,999032	491	0,999111
400	0,998938	446	0,999034	492	0,999112
401	0,99894	447	0,999036	493	0,999114
402	0,998943	448	0,999038	494	0,999115
403	0,998945	449	0,999040	495	0,999117
404	0,998947	450	0,999042	496	0,999118
405	0,99895	451	0,999043	497	0,99912
406	0,998952	452	0,999045	498	0,999121
407	0,998954	453	0,999047	499	0,999123
408	0,998956	454	0,999049	500	0,999124
409	0,998959	455	0,999051
410	0,998961	456	0,999052

Méthodes et formules pour Box-Cox

Formule de Box-Cox

Si vous utilisez une transformation de Box-Cox, Minitab transforme les valeurs de données d'origine (Y_i) conformément à la formule suivante :

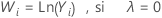
où λ est le paramètre de transformation. Minitab crée ensuite une carte de contrôle des valeurs de données transformées (W_i). Pour découvrir comment Minitab choisit la valeur optimale pour λ, accédez à Méthodes et formules pour la fonction Transformation de Box-Cox.

Valeurs courantes de λ

Le tableau suivant présente certaines valeurs courantes de λ et les transformations associées.

λ	Transformation
2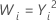
0,5
0
−0,5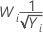
−1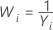

Méthodes et formules pour la fonction Cartes de contrôle des individus

Sur ce thème

Points relevés

Ligne centrale

Limites de contrôle

Limite de contrôle inférieure (LCI)

Limite de contrôle supérieure (LCS)

Notation

Méthode de la moyenne de l'étendue mobile

Notation

Estimations de Nelson

Méthode de la médiane de l'étendue mobile

Notation

Méthode pour la racine carrée de MSSD

Avec constante de correction de biais

Sans constante de correction de biais

Notation

Constantes de correction de biais d2(), d3() et d4()

Constante de correction de biais c4'()

Méthodes et formules pour Box-Cox

Formule de Box-Cox

Valeurs courantes de λ