d2(N) représente la valeur attendue pour l'étendue de N observations dans une population normale avec un écart type de 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors E(r) = d2(N)σ.
d3(N) représente l'écart type de l'étendue de N observations dans une population normale avec σ = 1. Ainsi, si r correspond à l'étendue d'un échantillon de N observations obéissant à une loi normale avec un écart type = σ, alors Ecart type(r) = d3(N)σ.
Utilisez le tableau suivant pour obtenir la constante de correction de biais pour une valeur donnée, N. (Pour déterminer la valeur de N, consultez la formule de la statistique correspondante.)

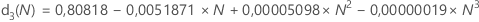
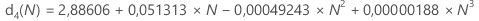
- D. J. Wheeler et D. S. Chambers (1992), Understanding Statistical Process Control, seconde édition, SPC Press, Inc.
- H. Leon Harter (1960), "Tables of Range and Studentized Range", The Annals of Mathematical Statistics, Vol. 31, No. 4, Institute of Mathematical Statistics, 1122−1147.
| N | d2(N) | d3(N) | d4(N) |
|---|---|---|---|
| 2 | 1,128 | 0,8525 | 0,954 |
| 3 | 1,693 | 0,8884 | 1,588 |
| 4 | 2,059 | 0,8798 | 1,978 |
| 5 | 2,326 | 0,8641 | 2,257 |
| 6 | 2,534 | 0,848 | 2,472 |
| 7 | 2,704 | 0,8332 | 2,645 |
| 8 | 2,847 | 0,8198 | 2,791 |
| 9 | 2,97 | 0,8078 | 2,915 |
| 10 | 3,078 | 0,7971 | 3,024 |
| 11 | 3,173 | 0,7873 | 3,121 |
| 12 | 3,258 | 0,7785 | 3,207 |
| 13 | 3,336 | 0,7704 | 3,285 |
| 14 | 3,407 | 0,763 | 3,356 |
| 15 | 3,472 | 0,7562 | 3,422 |
| 16 | 3,532 | 0,7499 | 3,482 |
| 17 | 3,588 | 0,7441 | 3,538 |
| 18 | 3,64 | 0,7386 | 3,591 |
| 19 | 3,689 | 0,7335 | 3,64 |
| 20 | 3,735 | 0,7287 | 3,686 |
| 21 | 3,778 | 0,7242 | 3,73 |
| 22 | 3,819 | 0,7199 | 3,771 |
| 23 | 3,858 | 0,7159 | 3,811 |
| 24 | 3,895 | 0,7121 | 3,847 |
| 25 | 3,931 | 0,7084 | 3,883 |
| N | d2(N) |
|---|---|
| 26 | 3,964 |
| 27 | 3,997 |
| 28 | 4,027 |
| 29 | 4,057 |
| 30 | 4,086 |
| 31 | 4,113 |
| 32 | 4,139 |
| 33 | 4,165 |
| 34 | 4,189 |
| 35 | 4,213 |
| 36 | 4,236 |
| 37 | 4,259 |
| 38 | 4,28 |
| 39 | 4,301 |
| 40 | 4,322 |
| 41 | 4,341 |
| 42 | 4,361 |
| 43 | 4,379 |
| 44 | 4,398 |
| 45 | 4,415 |
| 46 | 4,433 |
| 47 | 4,45 |
| 48 | 4,466 |
| 49 | 4,482 |
| 50 | 4,498 |
