Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Plan CUSUM, h, k et FIR
Dans les cas de procédés maîtrisés, les cartes CUSUM sont efficaces pour repérer de petits décalages par rapport à la cible, car elles intègrent des informations fournies par la suite des valeurs des échantillons. Les points relevés représentent les sommes cumulées des écarts des valeurs des échantillons par rapport à la cible. Ils doivent fluctuer de manière aléatoire autour de zéro. Si une tendance ascendante ou descendante se développe, elle doit être considérée comme une preuve que la moyenne du procédé s'est décalée et vous devez rechercher des causes spéciales.
- CUSUM tabulaire (par défaut)
- La CUSUM supérieure détecte les décalages ascendants du niveau du procédé et la CUSUM inférieure les décalages descendants. Cette carte utilise les limites de contrôle supérieure (LCS) et inférieure (LCI) pour déceler les situations hors contrôle. Pour une réflexion sur les CUSUM tabulaires, voir Prins et al.1 et Stoumbos et al.2.
- CUSUM à masque en V
- Cette carte utilise un masque en V, et non les limites de contrôle, pour déceler l'occurrence de situations hors contrôle. Pour débattre de la carte à masque en V, voir Lucas3 et Wadsworth et al.4
Les cartes CUSUM sont définies par deux paramètres, h et k, qui sont souvent appelés "plan CUSUM". Ces valeurs sont généralement sélectionnées à partir de tableaux ARL (Average Run Length, longueur moyenne d'essai). Voir Lucas3 et Lucas et al.5.
h
Pour les CUSUM tabulaires, h représente le nombre d'écarts types entre la ligne centrale et les limites de contrôle. Il s'agit de la valeur à laquelle un signal hors contrôle survient.
Pour les CUSUM à masque en V, Minitab calcule la demi-largeur du masque en V (H) au point origine, exprimée comme suit : H = hσ.
La valeur de h par défaut est 4.
k
Pour les CUSUM tabulaires, k représente la souplesse admise dans le procédé. Dans la formule pour les points d'une carte CUSUM, k définit l'importance du décalage à détecter.
Pour les CUSUM à masque en V, k est la pente des bras du masque en V. Vous pouvez sélectionner k dans une table ARL.
La valeur de k par défaut est 0,5.
FIR
La méthode FIR (pour fast initial response) est utilisée pour initialiser la CUSUM tabulaire. Normalement, les sommes cumulées de ce type sont initialisées à 0, mais si le procédé est hors contrôle au début, les CUSUM ne détecteront pas cette anomalie pour plusieurs sous-groupes.CUSUM tabulaire
Points relevés
Les données relevées dans une carte CUSUM représentent CInfi, CSupi.
Valeur d'une CUSUM tabulaire inférieure à l'instant i :
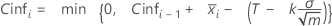
où :
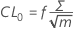
Valeur d'une CUSUM tabulaire supérieure à l'instant i :

où :

Ligne centrale
Par défaut, la valeur de la ligne centrale de la carte CUSUM tabulaire est 0.
Limite de contrôle inférieure (LCI)
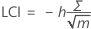
Limite de contrôle supérieure (LCS)
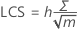
Notation
| Terme | Description |
|---|---|
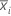 | moyenne de sous-groupe |
| T | cible |
| k | importance du décalage à détecter |
| σ | écart type du procédé |
| m | effectif du sous-groupe |
| f | FIR |
| h | intervalle de décision |
CUSUM à masque en V
Points relevés
Ci, la valeur d'une CUSUM à masque en V au moment i =
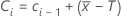
où C0 = 0
Pente du masque en V

Largeur à l'origine du masque en V
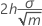
Origine du masque en V
La carte par défaut utilise n pour estimer l'origine p.
Notation
| Terme | Description |
|---|---|
| T | cible |
| k | pente du bras du masque en V |
| h | intervalle de décision |
| m | effectif du sous-groupe |
Méthodes et formules pour Box-Cox
Formule de Box-Cox
Si vous utilisez une transformation de Box-Cox, Minitab transforme les valeurs de données d'origine (Yi) conformément à la formule suivante :

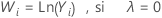
où λ est le paramètre de transformation. Minitab crée ensuite une carte de contrôle des valeurs de données transformées (Wi). Pour découvrir comment Minitab choisit la valeur optimale pour λ, accédez à Méthodes et formules pour la fonction Transformation de Box-Cox.
Valeurs courantes de λ
| λ | Transformation |
|---|---|
| 2 | 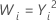 |
| 0,5 |  |
| 0 |  |
| −0,5 | 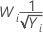 |
| −1 | 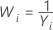 |
