Méthodes et formules pour la fonction Carte de variance généralisée

|S_i|, qui est le déterminant de la matrice de covariance de l’échantillon pour l’échantillon i.

S'il n'existe aucun sous-groupe, toutes les formules pour la carte de variance généralisée ne peuvent pas être calculées. Dans ce cas, Minitab normalise toutes les valeurs en soustrayant la moyenne de colonne appropriée, puis en divisant le résultat par la racine carrée de la variance appropriée à la matrice de covariance de toutes les données.

Lorsque les données sont dans des sous-groupes, le graphique affiche une valeur manquante pour tout sous-groupe qui est une observation individuelle. Le graphique affiche également une valeur manquante si la taille d’un sous-groupe est inférieure ou égale au nombre de variables sur le graphique.

Voir Montgomery¹ pour plus d’informations sur les graphiques de variance généralisée.

Limite de contrôle inférieure (LCI)

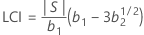
où :

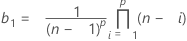
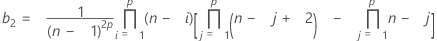
La valeur minimale de LCI est 0.

Limite de contrôle supérieure (LCS)

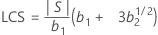
Notation

Formule de Box-Cox

Si vous utilisez une transformation de Box-Cox, Minitab transforme les valeurs de données d'origine (Y_i) conformément à la formule suivante :

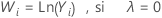
où λ est le paramètre de transformation. Minitab crée ensuite une carte de contrôle des valeurs de données transformées (W_i). Pour découvrir comment Minitab choisit la valeur optimale pour λ, accédez à Méthodes et formules pour la fonction Transformation de Box-Cox.

Valeurs courantes de λ

Le tableau suivant présente certaines valeurs courantes de λ et les transformations associées.

λ	Transformation
2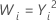
0,5
0
−0,5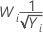
−1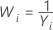