Sur ce thème
Points relevés
Les points relevés sur une carte quadratique T représentent les valeurs T2 pour chaque sous-groupe. Les points relevés sur une carte de variance généralisée représentent les statistiques de variance généralisée pour chaque sous-groupe.
Interprétation
Lorsqu'un procédé est maîtrisé, les points se trouvent en dessous de la limite de contrôle supérieure et la variation est uniquement due à des causes communes. Examinez les points situés au-dessus de la limite de contrôle supérieure. Les cartes multivariées présentent un inconvénient, à savoir que leur échelle n'est pas liée à celle de l'une des variables. De plus, les signaux hors contrôle ne révèlent pas la variable (ou la combinaison de variables) qui les a causés.
Ligne centrale
La ligne centrale de la carte quadratique T représente la médiane de la loi de distribution théorique des statistiques T2. La ligne centrale de la carte de variance généralisée est le déterminant de la matrice de covariance d'échantillon.
Interprétation
Appuyez-vous sur la ligne centrale pour observer le fonctionnement du procédé par rapport à la moyenne. Lorsqu'un procédé est maîtrisé, les points fluctuent de manière aléatoire autour de la ligne centrale.
Limites de contrôle
Les limites de contrôle sont les lignes horizontales situées au-dessus et en dessous de la ligne centrale. Les limites de contrôle indiquent si un procédé est maîtrisé et sont déterminées à partir de la variation observée à l'intérieur des sous-groupes et de la variation attendue des points représentés. La carte quadratique T dispose uniquement d'une limite de contrôle supérieure. La carte de variance généralisée a des limites de contrôle supérieure et inférieure.
Valeurs de statistique T2 décomposée
Les valeurs de la statistique T2 décomposée indiquent la contribution de chaque variable pour la totalité des points hors contrôle d'une carte T2.
Dans une carte T2, les différents points sont des valeurs composites qui représentent plusieurs variables. Par conséquent, la carte T2 n'indique pas la contribution de chacune des variables dans la valeur du point combinée, ce qui complique l'interprétation des points hors contrôle. Lorsqu'un point est hors contrôle sur une carte T2, vous ne pouvez pas déterminer quelles variables ont contribué à cette situation : toutes, certaines d'entre elles ou une seule d'entre elles. En revanche, les valeurs de T2 indiquent si une variable a plus contribué que d'autres au fait que le point soit hors contrôle.
Matrices de covariance
Une matrice de covariance est une matrice carrée qui comporte les variances et les covariances associées à plusieurs variables. Les éléments de diagonale de la matrice contiennent les variances des variables, tandis que les éléments hors diagonale contiennent les covariances entre toutes les paires possibles de variables.
La matrice de variance/covariance est symétrique car la covariance entre X et Y est identique à celle entre Y et X. Par conséquent, la covariance pour chaque paire de variables apparaît deux fois dans la matrice : la covariance entre les ie et je variables est affichée aux positions (i, j) et (j, i).
Après avoir stocké les matrices de covariance, sélectionnez pour les afficher.
Interprétation
| X | Y | Z | |
| X | 2,0 | −0,86 | −0,15 |
| Y | −0,86 | 3,4 | 0,48 |
| Z | −0,15 | 0,48 | 0,82 |
Les variances sont affichées en gras dans la diagonale. Les variances de X, Y et Z sont respectivement de 2,0, 3,4 et 0,82. La covariance entre X et Y est de −0,86, celle entre X et Z est de −0,15 et celle entre Y et Z est de 0,48.
Etapes
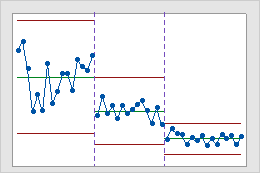
Utilisez des étapes pour créer une carte de contrôle historique qui montre l'évolution d'un procédé au cours de périodes spécifiques. A chaque étape, Minitab recalcule par défaut la ligne centrale et les limites de contrôle. Pour plus d'informations, reportez-vous à la rubrique Ajouter des étapes pour illustrer le changement d'un procédé.
Interprétation
Cette carte de contrôle historique montre trois étapes d'un procédé, qui représentent les situations avant, pendant et après la mise en œuvre d'une nouvelle procédure.