Sélectionnez la méthode ou la formule de votre choix.
Sur ce thème
Points relevés
Données en sous-groupes
Lorsque les données sont en sous-groupes, T2 est calculé comme suit:
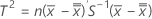
où :
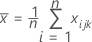
 est le vecteur moyen de
est le vecteur moyen de 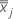 (moyenne de xvaleurs jk ), qui est calculée comme suit:
(moyenne de xvaleurs jk ), qui est calculée comme suit:
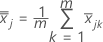
S = matrice de covariance d'échantillon
La matrice de covariance d'échantillon, S, est calculée comme suit :

où :
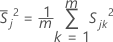
où :
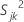 , la variance de l’échantillon pour la jème caractéristique du kème échantillon est calculée comme suit:
, la variance de l’échantillon pour la jème caractéristique du kème échantillon est calculée comme suit:
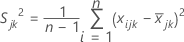
où :
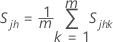
où :
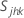 , la covariance, =
, la covariance, =
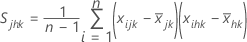
La moyenne des matrices S est une estimation sans biais de la variance lorsque le procédé est maîtrisé. n doit être supérieur à p et il ne doit exister aucune corrélation forte entre les variables afin que la matrice de covariance d'échantillon ne soit pas singulière.
Lorsque les données sont dans des sous-groupes, le graphique affiche une valeur manquante pour tout sous-groupe qui est une observation individuelle.
Observations individuelles
Lorsque les données sont des observations individuelles, T2 est calculé comme suit:
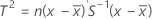
où :
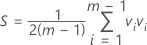
où :

Notation
| Terme | Description |
|---|---|
| n | effectif de l'échantillon |
 | vecteur de moyenne d'échantillon |
| xijk | La ième observation sur la jème caractéristique du kème échantillon |
| m | nombre d'échantillons |
Exemple de calcul de la valeur T2
Minitab représente la statistique T quadratique sur une carte de contrôle. Si un point relevé est en dehors des limites de contrôle, le procédé n'est pas maîtrisé au niveau de ce point. Pour plus d'informations sur les calculs Minitab, reportez-vous au tableau et aux exemples d'échantillon.
Les données suivantes proviennent du procédé de développement d'une solution de nettoyage. La quantité de citrate de sodium et de glycérol a une incidence sur la puissance de la solution.
| Moyennes des sous-groupes | Variances et covariances | Statistique T2 | ||||
| Sous-groupe | Citrate de sodium (X1) | Glycérol (X2) | S 1 2 | S2 2 | S 1 2 k | T2 |
| 1 | 125 | 025 | 7292 | 8692 | 5791 | 5708 |
| 2 | 625 | 4 | 2292 | 2333 | 3333 | 1429 |
| 3 | 4 | 875 | 1467 | 0625 | 8000 | 9528 |
| 4 | 2 | 2 | 2933 | 7600 | 6667 | 8073 |
| 5 | 25 | 225 | 2500 | 2692 | 7917 | 7548 |
| 6 | 4 | 45 | 6667 | 9567 | 3333 | 2711 |
| 7 | 275 | 025 | 3692 | 4692 | 7108 | 7785 |
| 8 | 6 | 65 | 4333 | 7700 | 6933 | 6183 |
| 9 | 625 | 325 | 7892 | 5558 | 1325 | 3592 |
| 10 | 3 | 5 | 2867 | 9467 | 2600 | 4942 |
| 11 | 25 | 5 | 1767 | 1200 | 9000 | 3279 |
| 12 | 1 | 625 | 1467 | 1692 | 4033 | 0277 |
| Moyennes | 7875 | 2333 | 7931 | 9318 | 3003 | |
- Calculez les moyennes des sous-groupes pour chaque variable, X1 et X2. Dans ce cas, chaque sous-groupe avait quatre échantillons.
- Dans le cas d'observations individuelles, Minitab utilise ces valeurs à la place des moyennes des sous-groupes dans tous les calculs.
- Calculez les variances des sous-groupes, S1 2 et S2 2.
- Calculez les covariances des sous-groupes, S1 2 k.
- Calculez la moyenne des moyennes des sous-groupes, la moyenne des variances des sous-groupes et la moyenne des covariances.
- Indiquez la matrice S de covariance d'échantillon et le vecteur moyen.
- Calculez la valeur T2, qui est obtenue de la façon suivante :
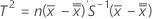
Minitab représente les valeurs T2 sur la carte T2 et les compare avec les limites de contrôle pour déterminer si des points individuels sont hors contrôle.
Ligne centrale
La ligne centrale pour la carte T2 est KX. Le calcul de K et de X dépend de l'effectif d'échantillon maximal et de si Minitab estime la matrice de covariance à partir des données.
Données en sous-groupes
Lorsque les données sont réparties en sous-groupes, KX est calculé comme suit :
- Matrice de covariance donnée
-


- Matrice de covariance estimée
-


Observations individuelles
Lorsque les données sont des observations individuelles, KX est calculé comme suit :
- Matrice de covariance donnée
-
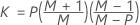
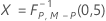
- Matrice de covariance estimée
-
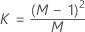
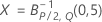
où :
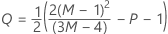
Notation
| Terme | Description |
|---|---|
| P | nombre de variables |
| M | nombre de sous-groupes |
| N | effectif d'échantillon |
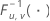 | loi F de répartition inverse avec u degrés de liberté pour le numérateur et v degrés de liberté pour le dénominateur |
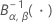 | loi bêta de répartition inverse où le premier paramètre de forme est α et le deuxième paramètre de forme est β |
Limite de contrôle
Données en sous-groupes
Si vous n'indiquez pas de paramètres, la limite de contrôle supérieure est définie comme suit :
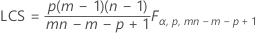
Si vous indiquez des paramètres, la limite de contrôle supérieure est définie comme suit :
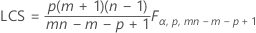
Observations individuelles
Si vous n'indiquez pas de paramètres, la limite de contrôle supérieure est définie comme suit :
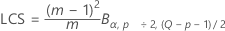
où :
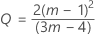
Reportez-vous à Woodall et al.1 pour plus d'informations.
Si vous indiquez des paramètres, la limite de contrôle supérieure est définie comme suit :
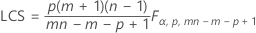
Notation
| Terme | Description |
|---|---|
| α | valeur fixée de 0,00134989803156746 |
| p | nombre de caractéristiques |
| m |
Pour les données en sous-groupes, si vous n'indiquez pas d'estimation des paramètres, m est le nombre d'échantillons. Si vous indiquez des estimations des paramètres, m est le nombre d'échantillons utilisés pour créer la matrice de covariance. Pour les données individuelles, m est le nombre d'observations. |
| n | effectif de chaque échantillon |
| F | indique que la loi F est utilisée |
| B | indique que la loi bêta est utilisée |
Statistique quadratique T2 décomposée
Statistique quadratique T2 décomposée :
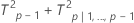
où :

où :
xi(p − 1) est le vecteur moyen décomposé
Sxx est la sous-matrice principale (p – 1) × (p – 1) de S
T2p|1,..., p−1 est une approximation qui varie selon les phases et selon le fait que vous disposiez de sous-groupes ou d'observations individuelles :
Phase 1 pour les données en sous-groupes
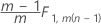
Phase 2 pour les données en sous-groupes
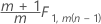
Phase 1 pour les observations individuelles
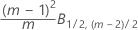
Phase 2 pour les observations individuelles
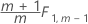
Minitab calcule les limites de contrôle pour la phase 1 lorsque vous n'indiquez pas d'estimation des paramètres, et les limites de contrôle pour la phase 2 lorsque vous en indiquez.
Pour plus d'informations sur la statistique quadratique T2 décomposée, reportez-vous à Mason et al.2
Notation
| Terme | Description |
|---|---|
| m | nombre d'échantillons |
| F | indique que la loi F est utilisée |
| B | indique que la loi bêta est utilisée |
Méthodes et formules pour Box-Cox
Formule de Box-Cox
Si vous utilisez une transformation de Box-Cox, Minitab transforme les valeurs de données d'origine (Yi) conformément à la formule suivante :

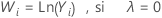
où λ est le paramètre de transformation. Minitab crée ensuite une carte de contrôle des valeurs de données transformées (Wi). Pour découvrir comment Minitab choisit la valeur optimale pour λ, accédez à Méthodes et formules pour la fonction Transformation de Box-Cox.
Valeurs courantes de λ
| λ | Transformation |
|---|---|
| 2 | 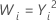 |
| 0,5 |  |
| 0 |  |
| −0,5 | 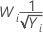 |
| −1 | 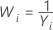 |
