Le rapport entre la variation observée et la variation attendue compare la variation dans vos données à la variation que vous attendriez avec une loi de Poisson. Le rapport est exprimé sous forme de pourcentage.
- Si le rapport est supérieur à la limite de confiance supérieure, vos données présentent alors une surdispersion significative.
- Si le rapport est inférieur à la limite de confiance inférieure, vos données présentent alors une sous-dispersion significative.
En cas de surdispersion, un nombre plus élevé de points peuvent se retrouver en dehors des limites de contrôle sur une carte U classique. A l'inverse, en cas de sous-dispersion, un nombre insuffisant de points peuvent apparaître hors des limites de contrôle sur une carte U classique. La carte U' de Laney offre un ajustement pour ces problèmes.
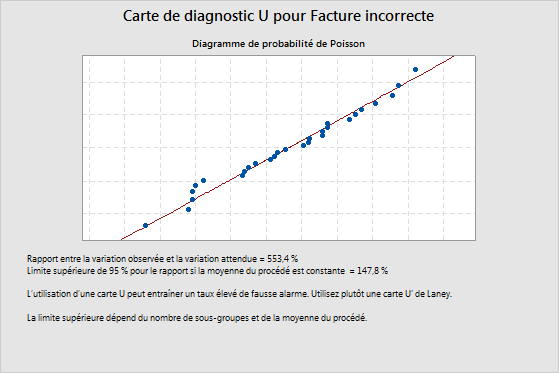
Exemple de surdispersion
Le rapport entre la variation observée et la variation attendue est de 553,4 %. Cette valeur indique la présence d'une surdispersion, car elle est supérieure à la limite de confiance supérieure, qui est de 147,8 %. En cas de surdispersion, les points d'une carte U traditionnelle peuvent sembler hors contrôle, alors qu'ils ne le sont pas. Pour ajuster la surdispersion, utilisez une carte U' de Laney.
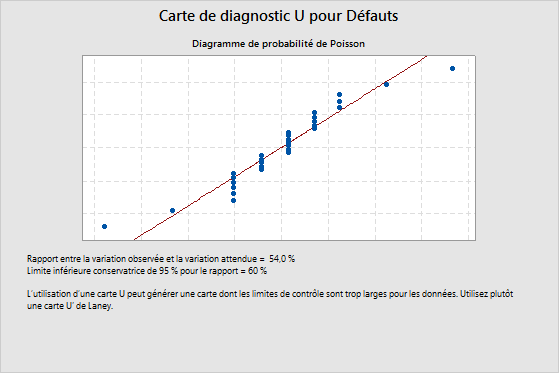
Exemple de sous-dispersion
Le rapport entre la variation observée et la variation attendue est de 54 %. Cette valeur indique la présence d'une sous-dispersion, car elle est inférieure à la limite de confiance inférieure, qui est de 60 %. En cas de sous-dispersion, les limites de contrôle peuvent paraître trop larges sur une carte U classique. Si les limites de contrôle sont trop larges, vous pouvez négliger une variation due à des causes spéciales et la prendre pour une variation due à des causes communes. Utilisez une carte U' de Laney afin d'effectuer un ajustement pour la sous-dispersion.