Sur ce thème
Points relevés
Dénombrements ajustés
Minitab calcule le nombre de non-conformes ajusté (ai) de la façon suivante :

Dénombrements transformés
Les dénombrements ajustés sont ensuite transformés à l'aide de la formule suivante :

Minitab crée ensuite une droite de Henry standard des dénombrements transformés à l'aide de la méthode indiquée dans .
Notation
| Terme | Description |
|---|---|
| di | nombre de non-conformes dans le sous-groupe i |
| ni | effectif du sous-groupe i |
 | effectif moyen des sous-groupes |
Rapport entre la variation observée et la variation attendue
Variation attendue
La variation attendue est égale à l'écart type des dénombrements transformés (Xi), qui est égal à 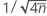 .
.
Variation observée
Afin de calculer la variation observée, Minitab calcule les scores normaux (Y) des dénombrements transformés de la façon suivante :

où NSCOR est la fonction Scores normaux (disponible en sélectionnant ).
Pour la prochaine étape, seuls les 50 % du milieu des valeurs Xi sont utilisés, ainsi que les valeurs Yi correspondantes. Les valeurs Xi sont exclues si elles sont inférieures au 25e percentile ou supérieures au 75e percentile.
Minitab ajuste un modèle de régression des moindres carrés avec Yi comme réponse et Xi comme prédicteur :
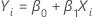
La variation observée est donc de 1 / β1.
Rapport
Le rapport entre la variation observée et la variation attendue est calculée de la façon suivante :
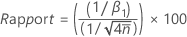
Notation
| Terme | Description |
|---|---|
| Xi | dénombrements transformés (pour plus d'informations, voir la section "Points relevés") |
 | effectif moyen des sous-groupes |
| β0 | ordonnée à l'origine de l'équation de régression des moindres carrés |
| β1 | coefficient de pente de l'équation de régression des moindres carrés |
Limites de confiance à 95 % pour le rapport
limite de confiance supérieure
La limite de confiance supérieure pour le rapport est calculée de la façon suivante :
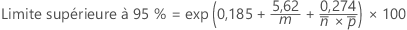
où  est la proportion moyenne de non-conformes, calculée de la façon suivante :
est la proportion moyenne de non-conformes, calculée de la façon suivante :

limite de confiance inférieure
Pour la limite de confiance inférieure du ratio, Minitab utilise une valeur prudente et fixe de 60 %.
Notation
| Terme | Description |
|---|---|
| m | nombre de sous-groupes |
 | effectif moyen des sous-groupes |
| di | nombre de non-conformes dans le sous-groupe i |
| ni | effectif du sous-groupe i |
Décision
- Si rapport > limite de confiance supérieure
- Si le rapport est supérieur à la limite de confiance supérieure, l'utilisation d'une carte P classique avec les données peut entraîner un taux de fausse alarme élevé. Dans ce cas, il est recommandé d'utiliser une carte P' de Laney.
- Si rapport < limite de confiance inférieure
- Si le rapport est inférieur à la limite de confiance inférieure, l'utilisation d'une carte P classique avec les données peut entraîner des limites de contrôle trop larges. Dans ce cas, il est recommandé d'utiliser une carte P' de Laney.
