Le superviseur d'un petit hôpital souhaite s'assurer que le nombre d'erreurs dans les dossiers médicaux de l'hôpital reste maîtrisé. Il enregistre le nombre total de dossiers archivés par jour et le nombre de dossiers incomplets ou inexacts (défectueux).
Le nombre de dossiers est élevé, avec un effectif de sous-groupe moyen supérieur à 2 500. Les données présentent une large surdispersion. Le superviseur décide donc d'utiliser une carte P' de Laney au lieu d'une carte P classique pour contrôler les dossiers des patients.
- Ouvrez le fichier de données échantillons, ErreurDossiers.MWX.
- Sélectionnez .
- Dans la zone Variables, saisissez Erronés.
- Dans la zone Effectifs de sous-groupes, saisissez Nb total dossiers.
- Cliquez sur Options de carte P′.
- Dans l'onglet Tests, sélectionnez 1 point > K écarts types à partir de la ligne centrale (test 1) et K points consécutifs, du même côté de la ligne centrale (test 2).Si vous n'êtes pas sûr des tests à appliquer, vous pouvez essayer d'utiliser les tests 1, 2 et 7 lorsque vous établissez pour la première fois les limites de contrôle en fonction de vos données.
- Cliquez sur OK dans chaque boîte de dialogue.
Interprétation des résultats
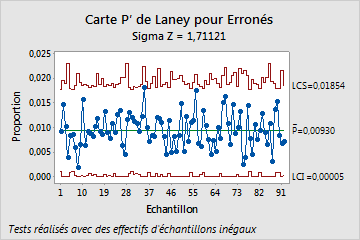
Les effectifs des échantillons étant inégaux, les limites de contrôle varient. La valeur Sigma Z (environ 1,7) est supérieure à 1, ce qui indique que les limites de contrôle de la carte P' de Laney sont plus larges que celles d'une carte P classique, afin qu'elles soient mieux ajustées à la surdispersion. Aucun des sous-groupes n'a échoué aux tests des causes spéciales, le superviseur en conclut donc que la proportion d'éléments non conformes est maîtrisée.