Qu'est-ce que la valeur de Z.référence ?
Vous pouvez utiliser des valeurs de Z.référence pour décrire la capabilité sigma de votre procédé. Etant donné qu'elles se fondent sur une loi de distribution normale standard, les statistiques Z.référence constituent des valeurs de référence qui permettent de comparer facilement la capabilité d'un procédé.
Pour comprendre la valeur de Z.référence, prenez en compte tous les défauts d'un procédé, qui se situent en général des deux côtés des limites de spécification.
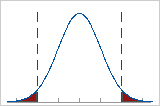
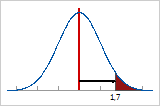
Si vous placez tous les défauts sur le côté droit de la distribution, puis mesurez le nombre d'écarts types à partir du centre vers le point qui définit le nombre total de défauts, vous obtenez la valeur de Z.référence.
Quelles sont les différentes valeurs de Z.référence ?
- Valeur de Z.référence à court terme (Z.référenceST)
- La valeur de Z.référence à court terme est calculée à l'aide de l'écart type "à l'intérieur" du procédé. Elle mesure les performances de votre procédé actuel si vous pouviez conserver la constante de variation à court terme, qui est idéale, ou la valeur de la validation du procédé.
- Valeur de Z.référence à long terme (Z.référenceLT)
- La valeur de Z.référence à long terme est calculée à l'aide de l'écart type global du procédé. Il s'agit d'une meilleure mesure de la réalité, car en règle générale nous ne pouvons pas maintenir la variation à court terme dans le temps. Elle représente la qualité que le client reçoit réellement.
- Décalage Z
- Il s'agit de la différence entre les valeurs de Z.référenceST et de Z.référenceLT. Plus le décalage Z est élevé, plus vous avez de possibilités d'amélioration si vous êtes en mesure de mieux contrôler votre procédé, et d'éliminer ou de réduire les causes spéciales qui provoquent la variation entre les sous-groupes.
Comment afficher la valeur de Z.référence ?
Vous pouvez effectuer une analyse de capabilité normale et afficher les statistiques Z.référence pour des données continues. Supposons que les données se trouvent dans la colonne C1, que l'effectif de sous-groupe soit de 5, que la limite de spécification inférieure soit de 598 et que la limite de spécification supérieure soit de 602. Partons également du principe que les données proviennent d'une distribution normale et que le procédé est maîtrisé.
- Sélectionnez .
- Dans la zone Colonne unique, saisissez C1.
- Dans la zone Effectif des sous-groupes, saisissez 5.
- Dans la zone Spécification inférieure, saisissez 598. Dans la zone Spécification supérieure, saisissez 602.
- Cliquez sur Options. Sélectionnez Z de référence (niveau de σ).
- Cliquez sur OK dans chaque boîte de dialogue.
Utilisation d'une valeur de Z.référence pour estimer la capabilité sigma
Les valeurs Z.référence sont souvent utilisées pour estimer la capabilité sigma d'un procédé. Toutefois, la méthode exacte utilisée peut différer en fonction des pratiques du secteur ou des normes de la société. Certains spécialistes présentent la capabilité sigma comme la valeur Z.référence à court terme sous Capabilité potentielle (à l'intérieur), qui utilise l'écart type dans des sous-groupes. D'autres définissent la capabilité sigma comme la valeur 1,5 plus la valeur Z.référence à long terme dans Capabilité globale, qui utilise l'écart type global du procédé. (Par exemple, si la valeur Z.référence sous Capabilité globale est égale à 4, la capabilité sigma est égale à 4 + 1,5 = 5,5.) Par conséquent, lors de la définition de la capabilité sigma, vous devez confirmer les lignes directrices spécifiques utilisées dans votre société ou votre secteur.
| Z.référence | Capabilité sigma | PPM de défectueux |
|---|---|---|
| 1 | 2,5 σ | 158 655 |
| 2 | 3,5 σ | 22 750 |
| 3 | 4,5 σ | 1 350 |
| 4 | 5,5 σ | 32 |
| 4,5 | 6,0 σ | 3,4 |
Remarque
Dans ce tableau, la capabilité sigma est calculée en supposant un décalage Z de 1,5σ.
