Indices de capabilité des données après transformation de Johnson
L'option Transformation de Johnson sélectionne de façon optimale une fonction parmi trois familles de distributions d'une variable, qui peuvent être facilement transformées en une distribution normale standard. Ces distributions sont intitulées SB, SL et SU, B, L et U désignant la variable affectée d'une borne, la variable log-normale et la variable libérée d'une borne. Dans Minitab, les paramètres des lois sont la première forme, la seconde forme, l'emplacement et l'échelle. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les transformations dans Identification de loi individuelle et cliquez sur "Méthodes et formules pour la transformation de Johnson".
Lorsque les deux limites de spécification se trouvent dans l'étendue de la fonction de transformation, Minitab calcule les indices de capabilité globale en fonction de la loi normale pour les données transformées. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les mesures de capabilité globale dans Analyse de capabilité normale.
Lorsque la famille sélectionnée est de type SB ou SL et que la limite de spécification inférieure et/ou supérieure se trouve en dehors de l'étendue de distribution, Minitab effectue des calculs supplémentaires pour générer les indices de capabilité globale .
Distribution SB
Si au moins une des limites de spécification (X) se trouve en dehors de l'étendue de distribution (pas ε < X < ε + λ) avant la transformation, les indices Pp, Ppk, PPI, PPS, Z.LSI et Z.LSS sont calculés comme suit.
Minitab commence par calculer les percentiles dans l'espace transformé.
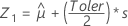
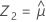
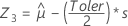
A l'aide des trois valeurs de Z, Minitab calcule les valeurs X1, X2 et X3 correspondantes dans l'espace d'origine :
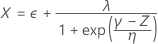
Les indices de capabilité globale sont ensuite calculés à partir des valeurs X et des valeurs des limites de spécification.
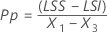
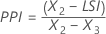
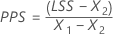



Notation
| Term | Description |
|---|---|
| LSI | Limite inférieure de spécification |
| LSS | Limite de spécification supérieure |
 | Moyenne d'échantillon (X̅) des données transformées |
| Toler | Tolérance dans les écarts types |
| s | Ecarts types d'échantillon des données transformées |
| ε | Paramètre d'emplacement de la transformation de Johnson |
| γ | Paramètre de forme de la transformation de Johnson |
| η | Paramètre de forme de la transformation de Johnson (η >0) |
| λ | Paramètre d'échelle de la transformation de Johnson (λ > 0) |
Les calculs des valeurs Z.référence et des performances attendues pour une distribution SB dépendent des emplacements de LSI et LSS par rapport à X2 et aux limites de distribution.
- Les indices LSI et LSS se trouvent du côté opposé de X2
-
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
La valeur Z.référence est manquante
PPM < LSI = 0
PPM > LSS = 0
PPM Total = 0
- Lorsqu'une limite de spécification se trouve en dehors de l'étendue de distribution et que l'autre limite de spécification se trouve à l'intérieur de l'étendue de distribution, Minitab calcule les valeurs suivantes :

PPM pour la limite de spécification en dehors de l'étendue = 0
PPM pour la limite de spécification à l'intérieur de l'étendue = p*1000000
PPM Total = p*1000000
Note
Minitab utilise les données transformées et les limites de spécification transformées pour calculer la valeur PPM.
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
- Les indices LSI et LSS se trouvent à gauche de la valeur X2
-
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
La valeur Z.référence est manquante
PPM < LSI = 0
PPM > USL = 1
PPM Total = 1
- Lorsque l'indice LSI se trouve en dehors de l'étendue de distribution et que la valeur LSS se trouve à l'intérieur de l'étendue de distribution, Minitab calcule les valeurs suivantes :

PPM < LSI = 0
PPM > LSS = p*1000000
PPM Total = PPM > LSS
Note
Minitab utilise les données et les limites de spécification transformées pour calculer la valeur PPM.
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
- Les indices LSI et LSS se trouvent à droite de la valeur X2
-
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
La valeur Z.référence est manquante
PPM < LSI = 1
PPM > LSS = 0
PPM Total = 1
- Lorsque l'indice LSI se trouve à l'intérieur de l'étendue de distribution et que l'indice LSS se trouve en dehors de l'étendue de distribution, Minitab calcule les valeurs suivantes.

PPM < LSL = p*1000000
PPM > LSS = 0
PPM Total = PPM < LSL
Note
Minitab utilise les données transformées et les limites de spécification transformées pour calculer la valeur PPM.
- Lorsque les indices LSI et LSS se trouvent en dehors de l'étendue de distribution, Minitab affiche les éléments suivants :
Distribution SL
Si au moins une des limites de spécification se trouve en dehors de l'étendue de distribution avant la transformation, Minitab utilise la même méthode que pour la distribution SB ci-dessus, afin de calculer les indices Pp, Ppk, PPI, PPS, Z.LSI et Z.LSS. Le seul changement réside dans la formule permettant d'obtenir la valeur X initiale à partir de la valeur Z transformée.

- Les indices LSI et LSS sont inférieurs ou égaux à ε (les deux valeurs se trouvent en dehors de l'étendue de distribution)
-
La valeur Z.référence est manquante
PPM < LSI = 0
PPM > USL = 1
PPM Total = 1
- L'indice LSI est inférieur ou égal à ε
-

PPM < LSI = 0
PPM > LSS = p*1000000
PPM Total = PPM > LSS
Notation
| Term | Description |
|---|---|
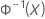 | Fonction de répartition (CDF) inverse d'une loi normale standard |
| p | Probabilité que les données transformées se trouvent en dehors de la limite de spécification transformée |
