Sur ce thème
Pp
Pp est calculé à l'aide des valeurs de paramètres spécifiées ou estimées à l'aide de la méthode du maximum de vraisemblance pour une loi de distribution utilisée dans l'analyse. Minitab calcule la statistique Pp à l'aide de la Méthode Z-score (par défaut) ou de la Méthode ISO, en fonction des paramètres sélectionnés dans . Les formules suivantes sont basées sur la tolérance par défaut K = 6, qui est de 6 écarts types de large (3 écarts types de chaque côté de la moyenne du procédé).
Méthode Z-score
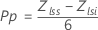
Notation
| Terme | Description |
|---|---|
| Zlsi | Φ–1(p1) |
| Zlss | Φ–1(p2) |
| Φ–1(p) | p * 100e percentile d'une loi normale standard |
| p1 | Prob (X ≤ LSI) |
| p2 | Prob (X ≤ LSS) |
| X | X suit la loi de distribution utilisée dans l'analyse |
Méthode ISO
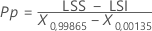
Notation
| Terme | Description |
|---|---|
| LSS | Limite de spécification supérieure |
| LSI | Limite inférieure de spécification |
| X0,99865 | Le 99,865e percentile de la loi de distribution spécifiée |
| X0,00135 | Le 0,135e percentile de la loi de distribution spécifiée |
L'indice Ppk

PPM Total pour les performances "globales" attendues
Le nombre attendu de pièces par million en dehors des limites de spécification est calculé comme suit :
PPM Total (Perf. globales attendues) = PPM < LSI (Perf. globales attendues) + PPM > LSS(Perf. globales attendues)
PPM Total (Perf. globales attendues) = [1 000 000 * F(LSI)]+ [1 000 000 * (1 – F(LSS))]
Notation
| Terme | Description |
|---|---|
| F(X) | Fonction de répartition (CDF) de la loi de distribution utilisée dans l'analyse en fonction des paramètres estimés ou spécifiés |
| LSI | Limite inférieure de spécification |
| LSS | Limite de spécification supérieure |
| PPM | Parties par million |
Z.référence Z.LSI Z.LSS
Pour calculer les statistiques Z de référence pour la capabilité globale, on détermine la valeur de Z à l'aide de la loi normale standard (0,1) pour les statistiques correspondantes.



Remarque
Les valeurs PPI et PPS sont basées sur la méthode (ISO ou Minitab) utilisée dans l'analyse. Pour plus d'informations, reportez-vous à la rubrique Méthodes et formules pour les mesures de capabilité globale dans Analyse de capabilité utilisant une loi non normale. Les formules sont basées sur la tolérance par défaut K = 6, qui est de 6 écarts types de large (3 écarts types de chaque côté de la moyenne du procédé).
Notation
| Terme | Description |
|---|---|
| P1 | Probabilité (observations < LSI) basée sur la loi non normale utilisée dans l'analyse et les paramètres que vous indiquez (ou les paramètres estimés à partir des données) |
| P2 | Probabilité (observations > LSS) basée sur la loi non normale utilisée dans l'analyse et les paramètres que vous indiquez (ou les paramètres estimés à partir des données) |
| Φ (X) | Fonction de répartition (CDF) d'une loi normale standard |
| Φ–1 (X) | CDF inverse d'une loi normale standard |
