Sur ce thème
Estimation de l'écart type
L'analyse entre/à l'intérieur repose sur les quatre écarts types suivants :
Ecart type dans les sous-groupes
σà l'intérieur est une estimation de la variation à l'intérieur des sous-groupes (par exemple, une équipe, un opérateur ou un lot de matériau). Minitab estime σà l'intérieur avec l'une des méthodes suivantes :
- Ecart type regroupé :

où :
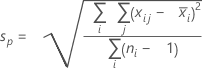
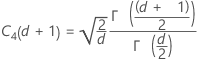
Remarque
Si vous changez la méthode par défaut et choisissez de ne pas utiliser la constante de correction de biais, σà l'intérieur est estimé par Sp.
Terme Description d Degrés de liberté pour Sp= Σ (ni- 1) Xij je observation du ie sous-groupe X̅i Moyenne du ie sous-groupe ni Nombre d'observations dans le ie sous-groupe C4(d+1) Constante de correction de biais Γ(·) Fonction gamma - Moyenne des étendues des sous-groupes (R barre) :

où :
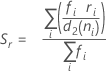
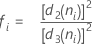
Si n sont tous les mêmes :

Terme Description ri Etendue du ie sous-groupe d2 (ni) Une constante de correction de biais lue à partir d'un tableau (pour plus d'informations, consultez la section Constantes de correction de biais d2(), d3() et d4() d3 (ni) Une constante de correction de biais lue à partir d'un tableau (pour plus d'informations, consultez la section Constantes de correction de biais d2(), d3() et d4() ni Nombre d'observations dans le ie sous-groupe - Moyenne des écarts types des sous-groupes (S barre) :

où :
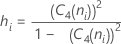
Remarque
Si vous changez le paramètre par défaut et n'utilisez pas la constante de correction de biais, σà l'intérieur est estimé par Σ Si / nombre de sous-groupes.
Terme Description C4(ni) Constante de correction de biais (telle que définie pour l'écart type regroupé) Si Ecart type du sous-groupe i ni Nombre d'observations dans le ie sous-groupe
Ecart type entre les sous-groupes
σEntre est une estimation de la variation entre les sous-groupes (par exemple, les sous-groupes collectés à des intervalles définis, par lots ou par des opérateurs différents).

- Moyenne de l'étendue mobile :

où :

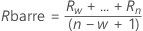
Terme Description Ri ième étendue mobile w Nombre d'observations utilisées dans l'étendue mobile. La valeur par défaut est w = 2. d2(w) Une constante de correction de biais lue à partir d'un tableau (pour plus d'informations, consultez la section Constantes de correction de biais d2(), d3() et d4() - Médiane de l'étendue mobile :

où :
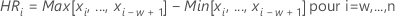
Terme Description EMi ième étendue mobile 
Médiane de l'EMi w Nombre d'observations utilisées dans l'étendue mobile. La valeur par défaut est w = 2. d4(w) Une constante de correction de biais lue à partir d'un tableau (pour plus d'informations, consultez la section Constantes de correction de biais d2(), d3() et d4() - Racine carrée de la moyenne des carrés des différences successives (MSSD) :
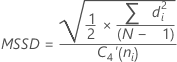
Remarque
Si vous changez le paramètre par défaut et n'utilisez pas la constante de correction de biais, σà l'intérieur est estimé par

Terme Description di Différences des moyennes de groupes successives C4(ni) Constante de correction de biais (telle que définie pour l'écart type regroupé) C4'(ni) Constante de correction de biais ≈ c4(ni). Pour plus d'informations, consultez la section Constante de correction de biais c4'(). N Nombre total d'observations ni Nombre d'observations dans le ie sous-groupe
Ecart type entre/à l'intérieur

| Terme | Description |
|---|---|
| σ2Entre | Variance entre les sous-groupes |
| σ2à l'intérieur | Variance à l'intérieur des sous-groupes |
Ecart type global

où :
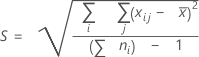
Remarque
Par défaut, Minitab n'utilise pas la constante de correction de biais lors de l'estimation de σglobal. σglobal est estimé par Si. Si vous souhaitez estimer l'écart type global à l'aide de la constante de correction de biais, vous pouvez modifier cette option dans la sous-boîte de dialogue Estimation lorsque vous effectuez l'analyse de capabilité. Si vous souhaitez que Minitab utilise toujours la constante de correction de biais par défaut, choisissez et sélectionnez les options voulues.
| Terme | Description |
|---|---|
| Xij | je observation dans le ie sous-groupe |
| X̅ | Moyenne du procédé |
| ni | Nombre d'observations dans le ie sous-groupe |
| C4 (N) | Constante de correction de biais (telle que définie pour l'écart type regroupé) |
| N (or Σ ni) | Nombre total d'observations |
Transformation de Box-Cox
La transformation de Box-Cox estime une valeur lambda, comme indiqué dans le tableau ci-dessous, qui réduit l'écart type d'une variable transformée normalisée. La transformation qui en résulte est Yλ lorsque λ ҂ 0 et ln Y lorsque λ = 0.
La méthode de Box-Cox effectue une recherche dans de nombreux types de transformations. Le tableau suivant présente des transformations courantes dans lesquelles Y' représente la transformation des données Y.
| Valeur lambda (λ) | Transformation |
|---|---|
 |
 |
 |
 |
 |
 |
 |
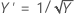 |
 |
 |
