Sur ce thème
Carte de contrôle des individus des moyennes de sous-groupe
La carte de contrôle des individus (I) représente les moyennes des sous-groupes. La ligne centrale est une estimation de la moyenne des moyennes des sous‑groupes. Les limites de contrôle, qui sont tracées à une distance de 3 écarts types au-dessus et au-dessous de la ligne centrale, présentent la variation attendue dans les moyennes des sous-groupes.
Pour Capability Sixpack entre/à l'intérieur, on utilise une carte I à la place d'une carte X barre, car les limites de contrôle de la carte I sont calculées à l'aide de la variation entre les sous-groupes, et non de la variation à l'intérieur des sous-groupes.
Interprétation
Utilisez la carte I pour surveiller la moyenne du procédé et déterminer s'il est suffisamment stable pour l'exécution d'une analyse de capabilité.
Les points rouges indiquent les observations qui ont échoué à au moins un test des causes spéciales et sont hors contrôle. Les points hors contrôle indiquent que le procédé n'est peut-être pas stable et que les résultats d'une analyse de capabilité ne sont peut-être pas fiables. Vous devez identifier la cause des points hors contrôle et éliminer la variation des causes spéciales avant d'analyser la capabilité du procédé.
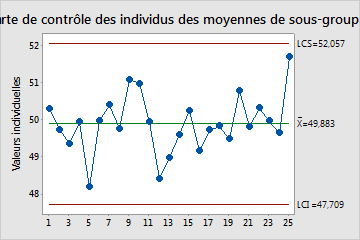
Dans cette carte, les points varient aléatoirement autour de la ligne centrale et se situent à l'intérieur des limites de contrôle. Cette carte ne présente ni tendance ni schéma. Le centre du procédé est suffisamment stable pour l'exécution d'une analyse de capabilité.
Carte d'étendue mobile des moyennes de sous-groupe
La carte EM permet de représenter les étendues mobiles des moyennes de sous-groupes consécutives. La ligne centrale indique la moyenne de toutes les étendues mobiles. Les limites de contrôle, qui sont tracées à une distance de 3 écarts types au-dessus et au-dessous de la ligne centrale, présentent la variation attendue dans les étendues mobiles.
Interprétation
Utilisez une carte EM pour surveiller la variation (étendue mobile) de votre procédé et déterminer s'il est suffisamment stable pour l'exécution d'une analyse de capabilité. Dans une analyse entre/à l'intérieur, la carte EM indique si la variation du procédé de sous-groupe à sous-groupe (entre des sous-groupes) est maîtrisée.
Les points rouges indiquent les observations qui ont échoué à au moins un test des causes spéciales et sont hors contrôle. Les points hors contrôle indiquent que le procédé n'est peut-être pas stable et que les résultats d'une analyse de capabilité ne sont peut-être pas fiables. Vous devez identifier la cause des points hors contrôle et éliminer la variation des causes spéciales avant d'analyser la capabilité du procédé.
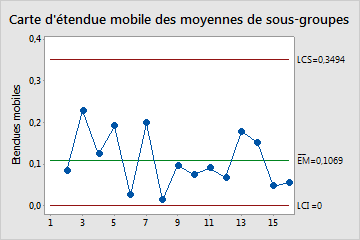
Dans ces résultats, les points varient aléatoirement autour de la ligne centrale et se situent à l'intérieur des limites de contrôle. Cette carte ne présente ni tendance ni schéma. La variation du procédé est suffisamment stable pour l'exécution d'une analyse de capabilité.
Carte d'étendue de toutes les données
La carte d'étendue (R) permet de représenter les étendues des sous-groupes. Si l'effectif de sous-groupe est constant, la ligne centrale sur la carte R représente la moyenne de toutes les étendues de sous-groupes. Si l'effectif de sous-groupe varie, la valeur de la ligne centrale dépend de l'effectif de sous-groupe, car des sous-groupes plus grands ont tendance à générer des étendues plus grandes. Les limites de contrôle, qui sont tracées à une distance de 3 écarts types au-dessus et au-dessous de la ligne centrale, présentent la variation attendue dans les étendues des sous-groupes.
Minitab affiche une carte R si l'effectif de sous-groupe est inférieur ou égal à 8. Si plus de 50 % des sous-groupes présentent le même effectif, l'effectif de sous-groupe le plus courant détermine la carte. Sinon, c'est l'effectif de sous-groupe le plus important qui détermine la carte.
Interprétation
Utilisez une carte R pour surveiller la variation d'un procédé et déterminer s'il est suffisamment stable pour l'exécution d'une analyse de capabilité. Dans une analyse entre/à l'intérieur, la carte R indique si la variation à l'intérieur des sous-groupes est maîtrisée.
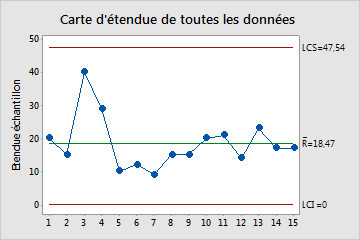
Dans ces résultats, les points varient aléatoirement autour de la ligne centrale et se situent à l'intérieur des limites de contrôle. Cette carte ne présente ni tendance ni schéma. La variation du procédé est suffisamment stable pour l'exécution d'une analyse de capabilité.
Carte S de toutes les données
La carte S représente les écarts types de sous-groupe. La ligne centrale représente la moyenne de tous les écarts types des sous-groupes. Les limites de contrôle, qui sont tracées à une distance de 3 écarts types au-dessus et au-dessous de la ligne centrale, présentent la variation attendue dans les écarts types des sous-groupes.
Minitab affiche une carte S pour surveiller la variation si votre effectif de sous-groupe est supérieur ou égal à 9. Si plus de 50 % des sous-groupes présentent le même effectif, l'effectif de sous-groupe le plus courant détermine la carte. Sinon, c'est l'effectif de sous-groupe le plus important qui détermine la carte.
Interprétation
Utilisez une carte S pour surveiller la variation (écart type) de votre procédé et déterminer s'il est suffisamment stable pour l'exécution d'une analyse de capabilité. Dans une analyse entre/à l'intérieur, la carte S indique si la variation à l'intérieur des sous-groupes est maîtrisée.
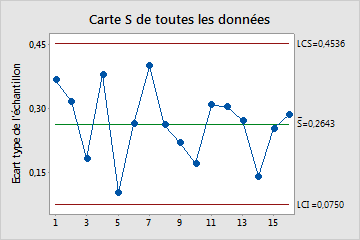
Dans ces résultats, les points varient aléatoirement autour de la ligne centrale et se situent à l'intérieur des limites de contrôle. Cette carte ne présente ni tendance ni schéma. La variation du procédé est suffisamment stable pour l'exécution d'une analyse de capabilité.
Tests des causes spéciales
Les tests des causes spéciales déterminent si les points tracés sur chaque carte de contrôle sont distribués aléatoirement à l'intérieur des limites de contrôle.
Interprétation
Utilisez les tests des causes spéciales pour identifier les observations que vous pouvez avoir besoin d'examiner et pour identifier des schémas et tendances spécifiques dans vos données. Chaque test des causes spéciales détecte un schéma ou une tendance spécifique dans vos données, ce qui révèle un aspect différent de l'instabilité du procédé.
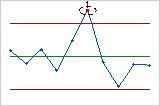
- Un point à plus de 3 écarts types de la ligne centrale
- Le test 1 indique les sous-groupes qui sont anormaux par rapport à d'autres. Le
test 1 est universellement reconnu comme nécessaire pour la détection de
situations non maîtrisées. Si vous souhaitez également détecter de
petits décalages dans le procédé, vous pouvez utiliser le test 2 en
supplément du test 1 pour créer une carte de contrôle plus sensible.
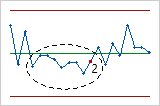
- Neuf points consécutifs du même côté de la ligne centrale
- Le test 2 identifie les décalages dans le centrage ou la variation du procédé. Si vous
souhaitez également détecter de petits décalages dans le procédé, vous
pouvez utiliser le test 2 en supplément du test 1 pour créer une carte
de contrôle plus sensible.
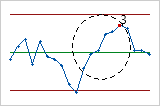
- Six points consécutifs, tous croissants ou tous décroissants
- Le test 3 détecte les tendances. Ce test recherche une longue série de points
consécutifs dont la valeur augmente ou diminue de façon constante.
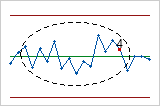
- Quatorze points consécutifs, croissants et décroissants en alternance
- Le test 4 détecte la variation systématique. Un point échouant au test 4 peut indiquer
que le modèle de variation est prévisible, alors que la variation doit
être aléatoire.
- Deux points sur trois à plus de 2 écarts types de la ligne centrale (côté identique)
- Le test 5 détecte les petits décalages dans le procédé.
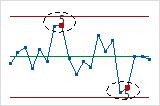
- Quatre points sur cinq à plus de 1 écart type de la ligne centrale (côté identique)
- Le test 6 détecte les petits décalages dans le procédé.
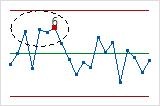
- 15 points consécutifs dans 1 écart type de la ligne centrale (des 2 côtés)
- Le test 7 détecte un schéma de variation qui est parfois confondu avec une indication
que le processus est maîtrisé. Ce test détecte les limites de contrôle
trop larges. En général, ces limites de contrôle trop larges sont dues à
des données stratifiées, en raison d'une source de variation
systématique dans chaque sous-groupe.
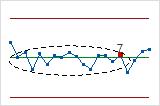
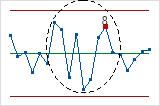
- 8 points consécutifs à plus de 1 écart type de la ligne centrale (des 2 côtés)
- Le test 8 détecte un schéma de mélange. Dans un schéma de mélange, les points tendent à
s'écarter de la ligne centrale pour se grouper près des limites de
contrôle.
Histogramme des capabilités
L'histogramme des capabilités présente la distribution de vos données échantillons. Chaque barre de l'histogramme représente la fréquence des données dans un intervalle.
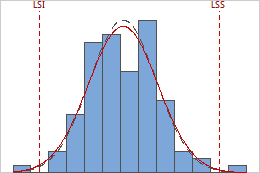
Les courbes entre/à l'intérieur et globale de l'histogramme sont des courbes de distribution normale générées à l'aide de la moyenne de procédé et de différentes estimations de la variation du procédé. La courbe entre/à l'intérieur (noire et en pointillés) utilise l'écart type entre/à l'intérieur des sous-groupes, tandis que la courbe globale (rouge) utilise l'écart type global.
Interprétation
Utilisez l'histogramme des capabilités pour visualiser vos données échantillons par rapport à l'ajustement de la loi de distribution et aux limites de spécification.
Pour évaluer visuellement l'ajustement de la loi de distribution, comparez les barres de l'histogramme à la ligne courbe. La forme des données de l'histogramme doit correspondre approximativement à la courbe. Pour vous assurer que les données suivent la loi, utilisez les résultats du diagramme de probabilité.
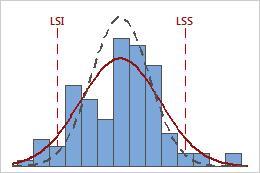
Dans ces résultats, les données du procédé semblent correctement centrées entre les limites de spécification. Toutefois, la dispersion du procédé est supérieure à la dispersion de spécification, ce qui suggère une faible capabilité. Bien que la plupart des données se trouvent dans les limites de spécification, il existe des éléments non conformes en dessous de la limite de spécification inférieure (LSI) et au-dessus de la limite de spécification supérieure (LSS).
Remarque
Pour déterminer le nombre d'éléments non conformes dans votre procédé, utilisez le résultat PPM global.
Diagramme de probabilité normale
- Ligne centrale
- Percentile attendu de la loi, en fonction des estimations des paramètres par le maximum de vraisemblance.
- Bornes de confiance
- La ligne courbe de gauche indique les bornes inférieures des intervalles de confiance pour les percentiles. La ligne courbe de droite indique les bornes supérieures des intervalles de confiance pour les percentiles.
- Statistique du test d'Anderson-Darling et valeur de p
- Résultats d'un test permettant de déterminer si vos données suivent la loi.
Interprétation
Utilisez le diagramme de probabilité normale pour évaluer l'exigence selon laquelle vos données suivent une distribution normale.
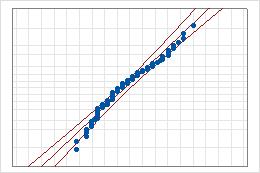
Si la loi normale est un bon ajustement pour les données, les points forment une ligne à peu près droite le long de la droite d'ajustement située entre les bornes de confiance. Des écarts par rapport à cette ligne droite indiquent des écarts par rapport à la normalité. Si la valeur de p est supérieure à 0,05, vous pouvez supposer que les données suivent la loi normale. Vous pouvez évaluer la capabilité de votre procédé à l'aide d'une loi normale.
Si la valeur de p est inférieure à 0,05, vos données ne sont pas normales et les résultats de l'analyse de capabilité peuvent être inexacts. Utilisez la commande Identification de loi individuelle pour déterminer si vous devez transformer les données ou ajuster une loi non normale pour effectuer l'analyse de capabilité.
Graphique des capabilités
Le graphique des capabilités se trouve dans le coin inférieur droit du rapport Capability Sixpack - Entre/A l'intérieur.
Le graphique des capabilités se compose de trois intervalles :
- L'intervalle entre/à l'intérieur représente la tolérance potentielle du procédé ; il est calculé en multipliant par six l'écart type entre et à l'intérieur.
- L'intervalle global représente la tolérance réelle du procédé et se calcule en multipliant par six l'écart type global.
- L'intervalle de spécifications est l'intervalle entre les limites de spécification inférieure et supérieure (LSI et LSS).
Le centre du procédé est indiqué par le repère à l'intérieur de l'intervalle de dispersion Global et E/I du procédé. La cible, le cas échéant, est indiquée par le repère situé à l'intérieur de la dispersion de spécification (Specs).
Interprétation
Utilisez le graphique des capabilités pour évaluer visuellement la capabilité de votre procédé.
Comparez l'intervalle entre/à l'intérieur et l'intervalle global à l'intervalle de spécifications. Pour un procédé ayant une bonne capabilité, l'intervalle entre/à l'intérieur et l'intervalle global doivent être plus étroits que l'intervalle de spécifications, et centrés sur la cible (le centre) des spécifications.
Comparez le centre du procédé à la cible, le cas échéant. Si le procédé est centré (sur la cible), les marqueurs de repères centraux correspondant aux spécifications et à la dispersion du procédé sont alignés à la verticale. Si le procédé n'est pas centré, examinez-en les motifs.
