Sur ce thème
PPM < LSI pour les performances observées
Le nombre de pièces sur un million dont les mesures sont inférieures à la limite de spécification inférieure est calculé comme suit :
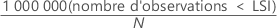
Notation
| Terme | Description |
|---|---|
| LSI | Limite inférieure de spécification |
| N | Nombre total d'observations |
PPM > LSS pour les performances observées
Le nombre de pièces sur un million dont les mesures sont supérieures à la limite de spécification supérieure est calculé comme suit :

Notation
| Terme | Description |
|---|---|
| LSS | Limite de spécification supérieure |
| N | Nombre total d'observations |
PPM Total pour les performances observées
Le nombre total de pièces par million en dehors des limites de spécification est calculé comme suit :


Notation
| Terme | Description |
|---|---|
| LSI | Limite inférieure de spécification |
| LSS | Limite de spécification supérieure |
| N | Nombre total d'observations |
Intervalles de confiance pour PPM et % hors spécification
Le calcul de l’intervalle de confiance est le même pour PPM et pourcentage, à l’exception d’une étape à la fin pour convertir le résultat en unités correctes. Les formules suivantes s’appliquent au 100(1 –  )% intervalles de confiance. Pour trouver des intervalles de confiance unilatéraux, remplacez
)% intervalles de confiance. Pour trouver des intervalles de confiance unilatéraux, remplacez 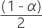 avec (1 –
avec (1 –  ).
).
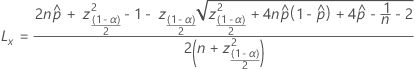
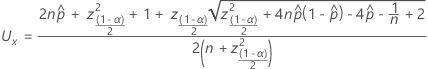
Pour convertir le résultat de la formule en PPM, multipliez par 1 000 000.
Pour convertir le résultat de la formule en pourcentage, multipliez par 100.
Si aucune unité observée n’est en dehors d’une limite de spécification, la limite de confiance inférieure est égale à 0. Si toutes les unités observées sont en dehors d’une limite de spécification, alors la limite de confiance supérieure est 1.
Notation
| Terme | Description |
|---|---|
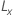 | Limite de confiance inférieure |
 | Limite de confiance supérieure |
| n | Nombre total d'unités |
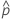 | Probabilité empirique qu’une unité soit hors spécification: défectueux / total. |
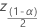 | (1 –  )/2 percentile à partir d’une distribution normale standard )/2 percentile à partir d’une distribution normale standard |
 | 1 – Le niveau de confiance |
Références
Newcombe, R. G. (1998). Two-sided confidence intervals for the single proportion: comparison of seven methods. Statistics in Medicine, 17(8), 857-872.
Tong, L. I., & Chen, J. P. (1998). Lower confidence limits of process capability indices for nonnormal process distributions. International Journal of Quality & Reliability Management, 15(8/9), 907-919.
