Sur ce thème
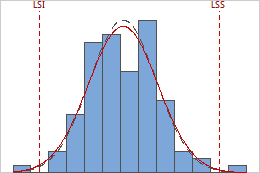
LSI
La limite de spécification inférieure (LSI) du procédé est la valeur minimale autorisée pour le produit ou service. Cette limite n'indique pas les résultats réels du procédé, mais les résultats que vous souhaitez qu'il atteigne. Vous indiquez la LSI lorsque vous configurez l'analyse de capabilité.
Remarque
Si vous utilisez une transformation de données lorsque vous effectuez l'analyse de capabilité, Minitab calcule également LSI*, c'est-à-dire la limite de spécification inférieure pour les données transformées.
Interprétation
Utilisez les limites LSI et LSS pour définir les exigences client et pour déterminer si votre procédé produit des éléments conformes à ces exigences.
Les limites de spécification inférieure et supérieure sont marquées par les lignes verticales en pointillés sur l'histogramme. Comparez les barres de l'histogramme aux lignes pour déterminer si les mesures se situent à l'intérieur des limites de spécification.
La dispersion de spécification correspond à la distance entre la limite de spécification inférieure (LSI) et limite de spécification supérieure (LSS). Supposons qu'une entreprise produise des stylos à bille et que le diamètre extérieur cible de la bille soit de 0,35 mm. L'étendue acceptable de diamètres extérieurs de la bille va de 0,34 à 0,36 mm. Par conséquent, la LSI est de 0,34, la LSS est de 0,36, et la dispersion de spécification est de 0,02 mm.
Minitab compare la dispersion de spécification à la dispersion du procédé pour déterminer la capabilité de celui-ci.
Cible
La cible est la valeur idéale d'un procédé, définie selon les exigences du client. Par exemple, si une pièce cylindrique offre des performances optimales dans un produit lorsque le diamètre est de 32 mm, la valeur de 32 mm correspond à la valeur cible pour cette pièce.
Interprétation
Utilisez la cible pour définir les exigences client et effectuer une comparaison avec vos observations.
La valeur cible est généralement (mais pas toujours) centrée entre les limites de spécification inférieure et supérieure. Lorsque vous avez une cible, regardez si votre procédé est centré près de la cible.
LSS
La limite de spécification supérieure (LSS) du procédé est la valeur maximale autorisée pour le produit ou service. Cette limite n'indique pas les résultats réels du procédé, mais les résultats que vous souhaitez qu'il atteigne. Vous indiquez la LSS lorsque vous configurez l'analyse de capabilité.

Remarque
Si vous utilisez une transformation de données lorsque vous effectuez l'analyse de capabilité, Minitab calcule également LSS*, c'est-à-dire la limite de spécification supérieure pour les données transformées.
Interprétation
Utilisez les limites LSI et LSS pour définir les exigences client et pour déterminer si votre procédé produit des éléments conformes à ces exigences.
Les limites de spécification inférieure et supérieure sont marquées par les lignes verticales en pointillés sur l'histogramme. Comparez les barres de l'histogramme aux lignes pour déterminer si les mesures se situent à l'intérieur des limites de spécification.
La dispersion de spécification correspond à la distance entre la limite de spécification inférieure (LSI) et limite de spécification supérieure (LSS). Supposons qu'une entreprise produise des stylos à bille et que le diamètre extérieur cible de la bille soit de 0,35 mm. L'étendue acceptable de diamètres extérieurs de la bille va de 0,34 à 0,36 mm. Par conséquent, la LSI est de 0,34, la LSS est de 0,36, et la dispersion de spécification est de 0,02 mm.
Minitab compare la dispersion de spécification à la dispersion du procédé pour déterminer la capabilité de celui-ci.
Moyenne de l'échantillon
La moyenne de l'échantillon est soit la moyenne des mesures d'échantillon, soit la moyenne du procédé historique que vous spécifiez pour l'analyse.
Interprétation
Utilisez la moyenne de l'échantillon pour estimer la valeur moyenne de votre procédé.
Vos données étant non normales et ne suivant peut-être pas une loi symétrique en forme de cloche, la moyenne d'échantillon peut ne pas survenir au pic de la distribution.
N de l'échantillon
L'effectif d'échantillon (N) correspond au nombre total d'observations dans les données. Par exemple, si vous avez collecté 20 sous-groupes d'effectif égal à 5, votre N de l'échantillon est de 100.
Interprétation
Utilisez N pour évaluer votre effectif d'échantillon.
En général, des effectifs d'échantillons plus grands produisent des estimations plus fiables de la capabilité de procédé. Certains experts recommandent au moins 100 observations totales pour une analyse de capabilité.
Forme
Le paramètre de forme d'une loi détermine la forme de la fonction de répartition. La forme est estimée à partir des données ou spécifiée sur la base des connaissances historiques sur le procédé.
Interprétation
Le paramètre de forme peut affecter la symétrie ou l'asymétrie des données.
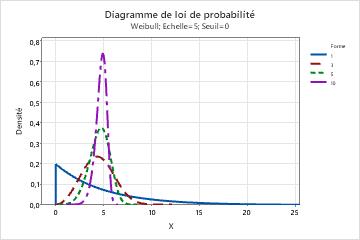
Effet du paramètre de forme pour une loi de Weibull
Ce graphique illustre l'effet de différentes valeurs du paramètre de forme sur la loi de Weibull.
Echelle
Le paramètre d'échelle d'une loi détermine l'échelle de la fonction de répartition. L'échelle est estimée à partir des données ou spécifiée sur la base des connaissances historiques sur le procédé.
Interprétation
Le paramètre d'échelle peut affecter le niveau de dispersion des données. En général, une valeur d'échelle supérieure peut entraîner un étirement horizontal de la distribution. Une valeur d'échelle réduite peut entraîner la compression horizontale de la distribution.
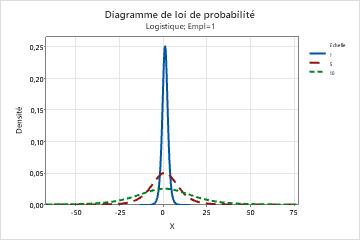
Effet du paramètre d'échelle pour une loi de distribution logistique
Ce graphique illustre l'effet de différentes valeurs du paramètre d'échelle sur la loi de distribution logistique.
Seuil
Le paramètre de seuil fournit une estimation de la valeur minimale d'une variable aléatoire. Le seuil est estimé à partir des données ou spécifié sur la base des connaissances historiques sur le procédé.
Interprétation
Le paramètre de seuil définit l'emplacement de la valeur minimale théoriquement possible pour les données à partir d'une loi de distribution.
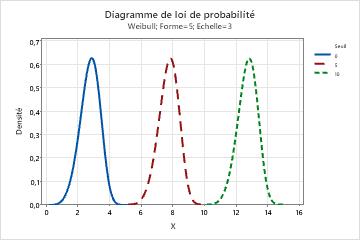
Effet du paramètre de seuil pour une loi de Weibull
Ce graphique illustre l'effet de différentes valeurs du paramètre de seuil sur la loi de Weibull.
Emplacement
Le paramètre d'emplacement affecte l'emplacement d'une loi de distribution. L'emplacement est estimé à partir des données ou spécifié sur la base des connaissances historiques sur le procédé.
Interprétation
Le paramètre d'emplacement peut affecter l'emplacement des données en les décalant le long de l'axe des X. Une valeur d'emplacement positive décale la distribution vers la droite, tandis qu'une valeur d'emplacement négative décale la distribution vers la gauche.
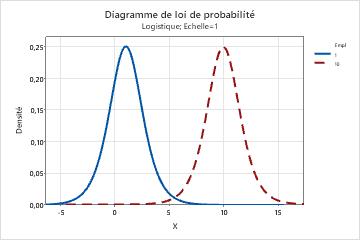
Effet du paramètre d'emplacement pour une loi de distribution logistique
Ce graphique illustre l'effet de différentes valeurs du paramètre d'emplacement sur la loi de distribution logistique.
Moyenne
Si vous utilisez la loi exponentielle pour modéliser vos données non normales, Minitab indique le paramètre de moyenne de la loi.
Interprétation
Le paramètre de moyenne définit la valeur centrale de la loi de distribution des données. Dans une loi exponentielle, la moyenne est égale au paramètre d'échelle lorsque le paramètre de seuil est égal à 0.
