Sur ce thème
Etape 1 : Déterminer si votre procédé est stable
Avant d'évaluer la capabilité de votre procédé, déterminez s'il est stable. Si votre procédé n'est pas stable, il se peut que les estimations de la capabilité du procédé ne soient pas fiables.
Utilisez la carte P pour surveiller visuellement le pourcentage de non-conformes et déterminer si le pourcentage de non-conformes est stable et maîtrisé.
Les points rouges indiquent les sous-groupes qui ont échoué à au moins un test des causes spéciales et sont hors contrôle. Les points hors contrôle indiquent que le procédé n'est peut-être pas stable et que les résultats d'une analyse de capabilité ne sont peut-être pas fiables. Vous devez identifier la cause des points hors contrôle et éliminer la variation des causes spéciales avant d'analyser la capabilité du procédé.
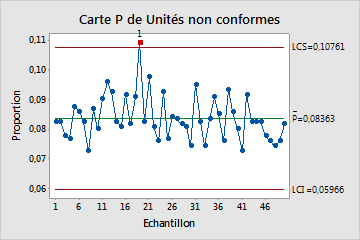
Dans cette carte P, la plupart des points varient aléatoirement et se situent à l'intérieur des limites de contrôle. Cette carte ne présente ni tendance ni schéma. La proportion d'unités non-conformes pour le jour 19 n'est pas maîtrisée. Avant d'évaluer la capabilité du procédé, étudiez les causes spéciales pouvant contribuer à un taux de non-conformes inhabituellement élevé ce jour-là et éliminez-les.
Etape 2 : Déterminer si les données suivent une loi binomiale
Avant d'évaluer la capabilité de votre procédé, déterminez s'il suit une loi binomiale. Si vos données ne suivent pas une loi binomiale, il se peut que les estimations de la capabilité du procédé ne soient pas fiables. Le graphique que Minitab affiche pour évaluer la loi des données varie selon que vos effectifs de sous-groupes sont égaux ou différents.
Effectifs de sous-groupes égaux
Si vos effectifs de sous-groupes sont tous égaux, Minitab affiche un diagramme binomial.
Etudiez le diagramme pour déterminer si les points relevés suivent à peu près une ligne droite. Si ce n'est pas le cas, l'hypothèse selon laquelle les données ont été échantillonnées à partir d'une loi de distribution binomiale est peut-être inexacte.
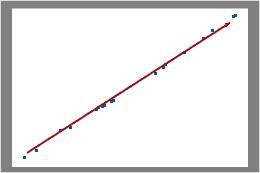
Binomiale
Dans ce diagramme, les points de données tombent près de la ligne. Vous pouvez considérer que les données suivent une loi binomiale.
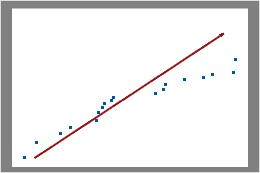
Non binomiale
Dans ce diagramme, les points de données ne tombent pas le long de la ligne, près de la partie supérieure droite. Ces données ne suivent pas une loi binomiale et ne peuvent pas être évaluées de manière fiable avec une analyse de capabilité binomiale.
Effectifs de sous-groupes différents
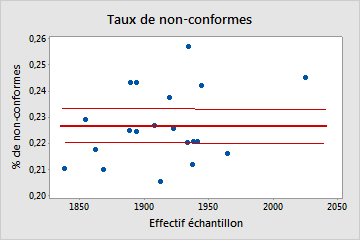
Si les effectifs de sous-groupes varient, Minitab affiche un diagramme du taux de non-conformes.
Etudiez le diagramme pour évaluer si le pourcentage de non-conformes est distribué de manière aléatoire pour les effectifs d'échantillons ou s'il existe un schéma. Si vos données sont réparties de manière aléatoire autour de la ligne centrale, vous en concluez que les données suivent une loi binomiale.
Binomiale
Dans ce diagramme, les points sont dispersés de manière aléatoire autour de la ligne centrale. Vous pouvez considérer que les données suivent une loi binomiale. Par conséquent, les données peuvent être évaluées avec une analyse de capabilité binomiale.
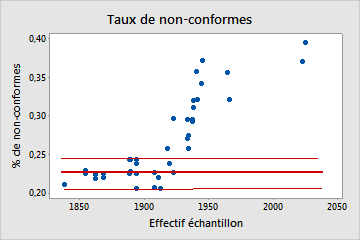
Non binomiale
Dans ce diagramme, le schéma n'est pas aléatoire. Pour des effectifs d'échantillons supérieurs à 1900, le pourcentage de défectueux augmente à mesure que l'effectif d'échantillon augmente. Ce résultat indique une corrélation entre l'effectif d'échantillon et le pourcentage de défectueux. Par conséquent, les données ne suivent pas une loi binomiale et ne peuvent pas être évaluées de manière fiable avec une analyse de capabilité binomiale.
Etape 3 : Evaluer le pourcentage d'unités défectueuses (non-conformes)
Examiner l'estimation et l'IC du pourcentage de non-conformes
Utilisez le pourcentage moyen de non-conformes des données échantillons pour estimer le pourcentage moyen de non-conformes du procédé. Utilisez l'intervalle de confiance comme marge d'erreur pour l'estimation.
L'intervalle de confiance fournit une étendue de valeurs probables pour la valeur réelle du pourcentage de non-conformes dans votre procédé (si vous pouvez collecter et analyser tous les éléments qu'il produit). Avec un niveau de confiance de 95 %, vous pouvez être certain à 95 % que le pourcentage de non-conformes du procédé se trouve dans l'intervalle de confiance. Ainsi, si vous collectez 100 échantillons aléatoires à partir de votre procédé, vous pouvez vous attendre à ce que 95 échantillons environ produisent des intervalles contenant la valeur réelle du pourcentage de non-conformes.
L'intervalle de confiance vous aide à évaluer la signification pratique de vos estimations d'échantillons. Si vous disposez d'une valeur maximale admissible pour le pourcentage de non-conformes fondée sur les normes du secteur ou sur votre connaissance du procédé, comparez la borne de confiance supérieure à cette valeur. Si la borne de confiance supérieure est inférieure à la valeur maximale admissible pour le pourcentage de non-conformes, vous pouvez être certain que votre procédé répond aux attentes, même en prenant en compte la variabilité de l'échantillonnage aléatoire qui affecte l'estimation.
| Statistiques récapitulatives | |
|---|---|
| (95,0 % de confiance) | |
| % de non-conformes : | 0,39 |
| IC inférieur : | 0,24 |
| IC supérieur : | 0,60 |
| Cible : | 0,50 |
| PPM de non-conformes : | 3 931 |
| IC inférieur : | 2 435 |
| IC supérieur : | 6 003 |
| Procédé Z : | 2,6579 |
| IC inférieur : | 2,5120 |
| IC supérieur : | 2,8155 |
Résultats principaux : % de non-conformes, IC
Les résultats de l'analyse de capabilité binomiale comprennent un tableau Statistiques récapitulatives, situé dans la partie centrale inférieure du résultat. Dans ce tableau Statistiques récapitulatives simulé, la cible (0,50 %) indique le pourcentage de non-conformes maximum admissible pour le procédé. L'estimation du pourcentage de non-conformes est de 0,39 %, ce qui est en dessous du pourcentage de non-conformes maximum admissible. Toutefois, l'IC supérieur pour le pourcentage de non-conformes est de 0,60 %, ce qui dépasse la valeur maximale admissible. Par conséquent, vous ne pouvez pas être certain à 95 % de la bonne capabilité du procédé. Vous devrez peut-être utiliser un effectif d'échantillon plus grand ou réduire la variabilité du procédé pour obtenir un intervalle de confiance plus étroit pour l'estimation du pourcentage de non-conformes.
Déterminez si vous avez disposez d'un nombre suffisant de données pour avoir une estimation fiable.
Utilisez le diagramme du pourcentage de non-conformes cumulé pour déterminer si vous avez disposez d'un nombre suffisant d'échantillons pour avoir une estimation stable du pourcentage de non-conformes.
Examinez le pourcentage de non-conformes des échantillons chronologiques pour déterminer l'évolution de l'estimation au fil des collectes d'échantillons. Idéalement, le pourcentage de non-conformes se stabilise après plusieurs échantillons, comme le montre l'aplatissement des points relevés le long de la ligne représentant le pourcentage moyen de non-conformes.
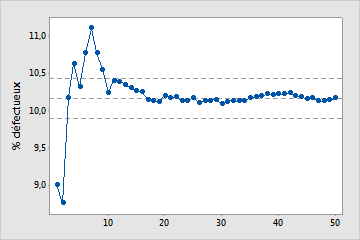
Assez d'échantillons
Dans ce diagramme, le pourcentage de non-conformes se stabilise le long de la ligne représentant le pourcentage moyen de non-conformes. Par conséquent, l'étude de capabilité comprend suffisamment d'échantillons pour produire une estimation stable et fiable du pourcentage moyen de non-conformes.
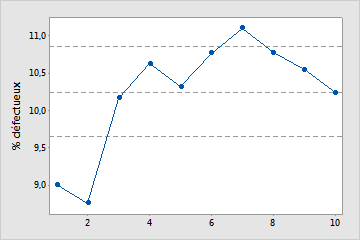
Pas assez d'échantillons
Dans ce diagramme, le pourcentage de non-conformes ne se stabilise pas. Par conséquent, cette étude de capabilité ne comprend pas suffisamment d'échantillons pour produire une estimation fiable du pourcentage moyen de non-conformes.
