Sur ce thème
Carte P
La carte P représente la proportion d'unités non conformes (également dites défectueuses) pour chaque sous-groupe. La ligne centrale représente la proportion moyenne de défauts dans tous les sous-groupes. Les limites de contrôle, qui sont tracées à une distance de 3 écarts types au-dessus et au-dessous de la ligne centrale, présentent la variation attendue dans les proportions des sous-groupes.
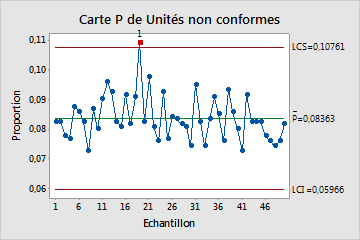
Cette carte P montre que, en moyenne, 8 % des éléments sont défectueux quel que soit le jour. La proportion d'unités défectueuses pour le jour 19 n'est pas maîtrisée, car sa valeur ne se situe pas dans les limites de la variation attendue.
Interprétation
Utilisez la carte P pour surveiller visuellement le pourcentage de non-conformes et déterminer si le pourcentage de non-conformes est stable et maîtrisé.
Les points rouges indiquent les sous-groupes qui ont échoué à au moins un test des causes spéciales et sont hors contrôle. Les points hors contrôle indiquent que le procédé n'est peut-être pas stable et que les résultats d'une analyse de capabilité ne sont peut-être pas fiables. Vous devez identifier la cause des points hors contrôle et éliminer la variation des causes spéciales avant d'analyser la capabilité du procédé.
Tests des causes spéciales
Les tests des causes spéciales déterminent si les points tracés sur chaque carte de contrôle sont distribués aléatoirement à l'intérieur des limites de contrôle.
Interprétation
Utilisez les tests des causes spéciales pour identifier les observations que vous pouvez avoir besoin d'examiner et pour identifier des schémas et tendances spécifiques dans vos données. Chaque test des causes spéciales détecte un schéma ou une tendance spécifique dans vos données, ce qui révèle un aspect différent de l'instabilité du procédé.
- Un point de plus que 3 sigmas à partir de la ligne centrale
- Le test 1 indique les sous-groupes qui sont anormaux par rapport à d'autres. Le test 1 est
universellement reconnu comme nécessaire pour la détection de situations
non maîtrisées. Si de petits décalages dans le procédé vous inquiètent,
vous pouvez utiliser le test 2 en supplément du test 1 pour créer une
carte de contrôle plus sensible.
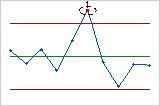
- Neuf points consécutifs du même côté de la ligne centrale
- Le test 2 identifie les décalages dans la variation du procédé. Si de petits décalages dans
le procédé vous inquiètent, vous pouvez utiliser le test 2 en supplément
du test 1 pour créer une carte de contrôle plus sensible.
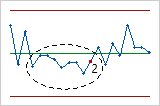
- Six points consécutifs, tous croissants ou tous décroissants
- Le test 3 détecte les tendances. Ce test recherche une longue série de points consécutifs
dont la valeur augmente ou diminue de façon constante.
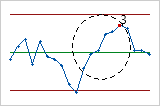
- Quatorze points consécutifs, croissants et décroissants en alternance
- Le test 4 détecte la variation systématique. Le schéma de variation d'un procédé doit
normalement être aléatoire, mais un point échouant au test 4 peut
indiquer que le schéma de variation est prévisible.
Diagramme de pourcentage de non-conformes cumulé
Les points situés sur le diagramme de pourcentage de non-conformes cumulé montrent le pourcentage moyen de non-conformes pour chaque échantillon. Les points sont affichés dans l'ordre dans lequel les échantillons ont été collectés. La ligne horizontale médiane représente le pourcentage moyen de non-conformes calculé à partir de tous les échantillons. Les lignes horizontales supérieure et inférieure représentent les bornes de confiance supérieure et inférieure pour le pourcentage moyen de non-conformes.
Interprétation
Utilisez le diagramme du pourcentage de non-conformes cumulé pour déterminer si vous avez disposez d'un nombre suffisant d'échantillons pour avoir une estimation stable du pourcentage de non-conformes.
Examinez le pourcentage de non-conformes des échantillons chronologiques pour déterminer l'évolution de l'estimation au fil des collectes d'échantillons. Idéalement, le pourcentage de non-conformes se stabilise après plusieurs échantillons, comme le montre l'aplatissement des points relevés le long de la ligne représentant le pourcentage moyen de non-conformes.
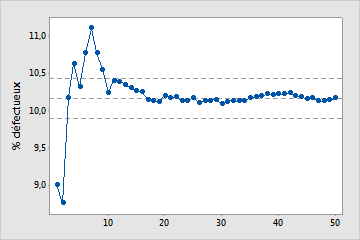
Assez d'échantillons
Dans ce diagramme, le pourcentage de non-conformes se stabilise le long de la ligne représentant le pourcentage moyen de non-conformes. Par conséquent, l'étude de capabilité comprend suffisamment d'échantillons pour produire une estimation stable et fiable du pourcentage moyen de non-conformes.
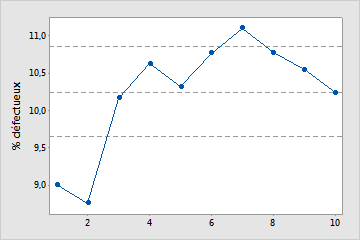
Pas assez d'échantillons
Dans ce diagramme, le pourcentage de non-conformes ne se stabilise pas. Par conséquent, cette étude de capabilité ne comprend pas suffisamment d'échantillons pour produire une estimation fiable du pourcentage moyen de non-conformes.
Diagramme binomial
Le diagramme binomial présente le nombre observé d'éléments non conformes par rapport au nombre attendu d'éléments non conformes. La ligne diagonale indique l'endroit où les données tomberaient si elles suivaient parfaitement la loi binomiale. Si les données s'écartent significativement de cette ligne, l'analyse de capabilité binomiale risque de produire des résultats peu fiables.
Remarque
Minitab affiche un diagramme binomial lorsque les effectifs de sous-groupes sont égaux. Si les effectifs de sous-groupes varient, Minitab affiche un diagramme du taux de non-conformes. Pour plus d'informations, consultez la section sur le diagramme du taux de non-conformes.
Interprétation
Utilisez le diagramme binomial pour déterminer si vos données suivent une loi binomiale.
Etudiez le diagramme pour déterminer si les points relevés suivent à peu près une ligne droite. Si ce n'est pas le cas, l'hypothèse selon laquelle les données ont été échantillonnées à partir d'une loi de distribution binomiale est peut-être inexacte.
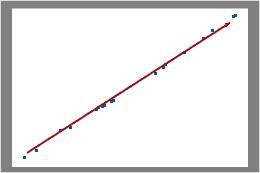
Dans ce diagramme, les points de données tombent près de la ligne. Vous pouvez considérer que les données suivent une loi binomiale.
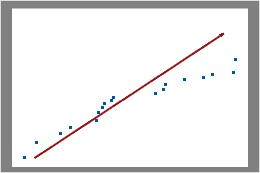
Dans ce diagramme, les points de données ne tombent pas le long de la ligne, près de la partie supérieure droite du diagramme. Ces données ne suivent pas une loi binomiale et ne peuvent pas être évaluées de manière fiable avec une analyse de capabilité binomiale.
Important
Si les points ne suivent pas une ligne droite, il se peut que la loi binomiale ne convienne pas à vos données et que l'analyse de capabilité ne soit pas valide.
Diagramme du taux de non-conformes
Le diagramme du taux de non-conformes affiche le pourcentage d'éléments non conformes dans un sous-groupe (% de non-conformes) et l'effectif de chaque sous-groupe. La ligne centrale représente la probabilité moyenne qu'un élément soit non conformes. Les bornes de confiance de la moyenne sont affichées au-dessus et en dessous de la ligne centrale.
Remarque
Minitab affiche un diagramme du taux de non-conformes lorsque l'effectif des sous-groupes varie. Si les effectifs de sous-groupes sont constants, Minitab affiche un diagramme de binomial. Pour plus d'informations, consultez la section sur le diagramme binomial.
Interprétation
Utilisez le diagramme du taux de non-conforme pour vérifier que vos données sont binomiales en vérifiant l'hypothèse selon laquelle la probabilité d'un élément non conformes est constante dans différents effectifs d'échantillons.
Etudiez le diagramme pour évaluer si le pourcentage de non-conformes est distribué de manière aléatoire pour les effectifs d'échantillons ou s'il existe un schéma. Si vos données sont réparties de manière aléatoire autour de la ligne centrale, vous en concluez que les données suivent une loi binomiale.
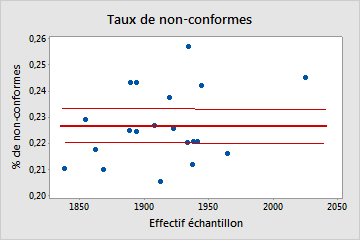
Binomiale
Dans ce diagramme, les points sont dispersés de manière aléatoire autour de la ligne centrale. Vous pouvez considérer que les données suivent une loi binomiale.
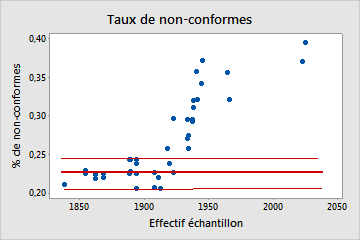
Non binomiale
Dans ce diagramme, le schéma n'est pas aléatoire. Pour des effectifs d'échantillon supérieurs à 1 900, le pourcentage de non-conformes augmente à mesure que l'effectif d'échantillon augmente. Ce résultat suggère une corrélation entre l'effectif d'échantillon et le pourcentage de non-conformes. Par conséquent, les données ne suivent pas une loi binomiale et ne peuvent pas être évaluées de manière fiable avec une analyse de capabilité binomiale.
Histogramme
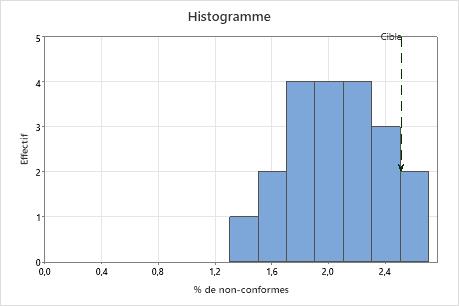
Interprétation
Utilisez l'histogramme du pourcentage de non-conformes pour évaluer la distribution du pourcentage de non-conformes dans vos échantillons.
Examinez le pic et la dispersion de la distribution du pourcentage de non-conformes. Le pic représente les valeurs les plus courantes et les approximations du centre du pourcentage de non-conformes. Evaluez la dispersion pour comprendre la variation du pourcentage de non-conformes dans vos échantillons.
Comparez la ligne de référence de la valeur cible aux barres de l'histogramme. Si votre procédé présente une bonne capabilité, la plupart ou la totalité des barres de l'histogramme doivent se situer à gauche de la valeur cible.
% de non-conformes
Le pourcentage de non-conformes (% de non-conformes) correspond au pourcentage moyen des éléments inacceptable dans vos échantillons. Les autres éléments peuvent être classés comme "acceptable" ou "bon".
Interprétation
Utilisez % de non-conformes pour déterminer si votre procédé répond aux exigences du client.
Comparez la cible de % de non-conformes au % de non-conformes pour déterminer si le procédé répond aux exigences. Si le pourcentage de non-conformes est supérieur à la cible, vous devez améliorer votre procédé.
Vous devez également comparer la cible à la limite de confiance supérieure du pourcentage de non-conformes. Si la limite de confiance supérieure est supérieur à la cible, vous ne pouvez pas être certain que le pourcentage de non-conformes du procédé est inférieur à la cible. Vous aurez peut-être besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si votre procédé est ciblé.
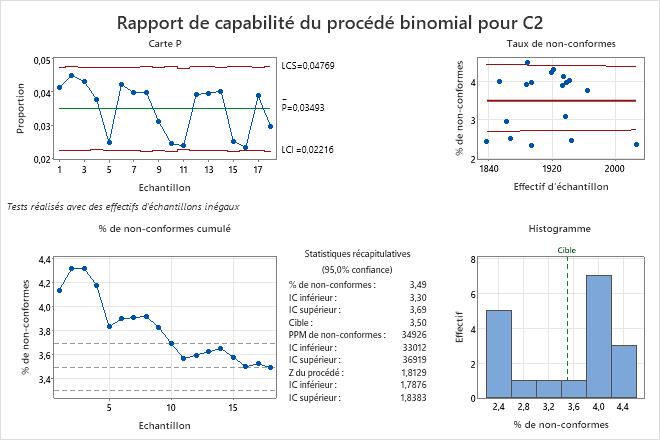
Par exemple, supposons que le pourcentage de non-conformes d'un procédé de service client ne doive pas dépasser 3,5 %. Dans le tableau Statistiques récapitulatives, le pourcentage de non-conformes est de 3,49 %, ce qui est inférieur à la cible. Toutefois, l'IC supérieur du pourcentage de non-conformes est de 3,69 %, ce qui est supérieur à la cible. Bien que l'estimation du pourcentage de non-conformes soit inférieure à la cible, vous avez besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si le pourcentage de non-conformes répond aux exigences du client.
Cible
La cible de % de non-conformes correspond au pourcentage maximum de non-conformes que vous êtes prêt à accepter. Si vous n'avez spécifié aucune cible, Minitab utilise une cible de 0 % de non-conformes.
Interprétation
Comparez la cible de % de non-conformes au % de non-conformes pour déterminer si le procédé répond aux exigences. Si le pourcentage de non-conformes est supérieur à la cible, vous devez améliorer votre procédé.
Vous devez également comparer la cible à la limite de confiance supérieure du pourcentage de non-conformes. Si la limite de confiance supérieure est supérieur à la cible, vous ne pouvez pas être certain que le pourcentage de non-conformes du procédé est inférieur à la cible. Vous aurez peut-être besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si votre procédé est ciblé.

Par exemple, dans le tableau Statistiques récapitulatives, le pourcentage de non-conformes est de 3,46 %, ce qui est inférieur à la cible (3,50 %). Toutefois, l'IC supérieur du pourcentage de non-conformes est de 3,66 %, ce qui est supérieur à la cible. Bien que le procédé semble répondre aux exigences, vous avez besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si le pourcentage de non-conformes est inférieur à la cible.
PPM de non-conformes
L'indice PPM de non-conformes évalue le nombre d'unité par million que vous pouvez vous attendre à trouver défectueuses. Si vous collectez un échantillon de 1 000 000 d'éléments à partir du procédé actuel, la valeur de PPM de non-conformes correspond au nombre approximatif de non-conformes dans l'échantillon.
Interprétation
Comparez la valeur PPM de non-conformes aux exigences du client pour déterminer si votre procédé nécessite une amélioration.
Vous devez également examiner la limite de confiance supérieure de PPM de non-conformes. Si la limite de confiance supérieure est supérieure à la valeur maximale admissible, vous ne pouvez pas être certain que votre procédé répond aux exigences du client. Vous aurez peut-être besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si votre procédé répond aux exigences du client.

Par exemple, dans le tableau Statistiques récapitulatives, le PPM de non-conformes est de 34 926. Si le client exige que le PPM de non-conformes soit inférieur à 35 000, le procédé répond aux exigences. Toutefois, l'IC supérieur est de 36 919, ce qui est supérieur à l'exigence du client. Par conséquent, vous avez besoin d'un effectif d'échantillon plus grand pour déterminer avec plus de certitude si le procédé est acceptable.
Z du procédé
La valeur Z du procédé correspond au point qui figure sur une loi de distribution normale standard N (0, 1) de telle sorte que la zone située à droite de ce point soit égale à la moyenne P (la proportion d'unités défectueuses dans votre procédé).
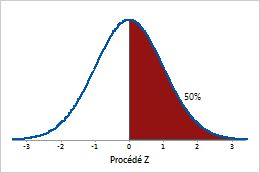
Une valeur Z du procédé de 0 correspond à 50 % de non-conformes.
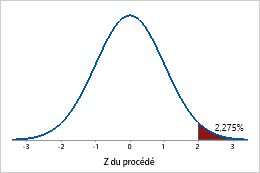
Une valeur Z du procédé de 2 correspond à 2,275 % de non-conformes.
Interprétation
Utilisez la valeur Z du procédé pour évaluer la capabilité sigma d'un procédé binaire.
Plus la valeur de Z est élevée, meilleures sont les performances du procédé. Idéalement, vous souhaitez une valeur Z du procédé d'au moins 2. La valeur cible de votre procédé dépend des conséquences d'une non-conformité pour votre client.
Intervalle de confiance (IC)
L'intervalle de confiance est une étendue de valeurs probables pour un indice de capabilité. L'intervalle de confiance est défini à l'aide d'une borne inférieure et d'une borne supérieure. Les bornes sont calculées à partir d'une marge d'erreur déterminée pour l'estimation de l'échantillon. La limite de confiance inférieure définit une valeur à laquelle l'indice de capabilité est susceptible d'être supérieur. La limite de confiance supérieure définit une valeur à laquelle l'indice de capabilité est susceptible d'être inférieur.
Minitab affiche une borne de confiance inférieure et une borne de confiance supérieure pour le pourcentage de non-conformes, le PPM de non-conformes et le procédé Z.
Interprétation
Etant donné que les échantillons de données sont aléatoires, différents échantillons collectés à partir du procédé peuvent générer des estimations identiques d'un indice de capabilité. Pour calculer la valeur réelle de l'indice de capabilité de votre procédé, il faudrait analyser les données de tous les éléments produits par le procédé, ce qui est impossible. En revanche, vous pouvez utiliser un intervalle de confiance pour déterminer une étendue de valeurs probables pour l'indice de capabilité.
Avec un niveau de confiance de 95 %, vous pouvez être certain à 95 % que la valeur réelle de l'indice de capabilité se trouve dans l'intervalle de confiance. Ainsi, si vous collectez 100 échantillons aléatoires à partir de votre procédé, vous pouvez vous attendre à ce que 95 échantillons environ produisent des intervalles contenant la valeur réelle de l'indice de capabilité.
L'intervalle de confiance vous aide à évaluer la signification pratique de vos estimations d'échantillons. Si possible, comparez les bornes de confiance à une valeur de référence fondée sur les normes du secteur ou sur votre connaissance du procédé.
Par exemple, le taux de défauts maximal admissible pour un procédé de fabrication est de 0,50 % de non-conformes. A l'aide de l'analyse de capabilité binomiale, les analystes obtiennent une estimation du pourcentage de non-conformes de 0,31 %, ce qui suggère que le procédé présente une bonne capabilité. La borne supérieure du pourcentage de non-conformes est de 0,48 %. Par conséquent, les analystes peuvent être sûrs à 95 % que la valeur réelle du pourcentage de non-conformes ne dépasse pas la valeur maximale admissible, même en prenant en compte la variabilité de l'échantillonnage aléatoire qui affecte l'estimation.
