Sur ce thème
- PPM < LSI pour les performances globales attendues
- PPM > LSS pour les performances globales attendues
- PPM Total pour les performances globales attendues
- Intervalles de confiance de la valeur PPM totale pour les performances globales attendues lorsque la LSI et la LSS sont toutes les deux connues
- Intervalles de confiance de la valeur PPM totale pour les performances globales attendues dans un procédé incluant une limite de spécification
PPM < LSI pour les performances globales attendues
PPM < LSI et % < LSI sont des multiples de la probabilité :
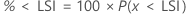
Intervalles de confiance bilatéraux
Les intervalles de confiance pour P(x < LSI) sont obtenus à l'aide des formules suivantes :
où
Les intervalles de confiance pour PPM < LSI et % < LSI sont déterminés en multipliant les intervalles de confiance de la probabilité par une constante.
PPM
%
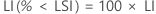
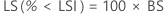
Borne de confiance unilatérale
Pour une borne unilatérale, les calculs sont les suivants :
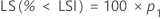
Minitab résout l'équation suivante pour trouver p1 :
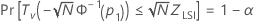
où
Notation
| Terme | Description |
|---|---|
| LSI | limite de spécification supérieure |
| LSS | limite de spécification supérieure |
| LI | borne inférieure |
| LS | borne supérieure |
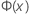 | fonction de répartition (CDF) obtenue avec la loi normale standard |
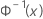 | CDF inverse obtenue avec la loi normale standard |
 | (1 - α/2)ème percentile de la loi normale standard |
| α | alpha du niveau de confiance |
 | moyenne du procédé (estimée à partir des données échantillons ou d'une valeur historique) |
| s | écart type global d'échantillon |
| N | nombre total de mesures |
| υ | degrés de liberté pour s |
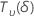 | variable aléatoire distribuée selon une loi t, avec  degrés de liberté et dotée du paramètre de non-centralité δ |
PPM > LSS pour les performances globales attendues
La proportion d'éléments excédant la limite de spécification supérieure, qu'elle soit exprimée en PPM (PPM > LSS) ou en pourcentage (% > LSS), est calculée à partir de la probabilité qu'une pièce se trouve au-dessus de la limite de spécification. (P(x > LSS)).
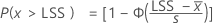
PPM > LSS et % > LSS sont des multiples de la probabilité :
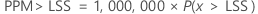
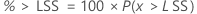
Intervalles de confiance bilatéraux
Les intervalles de confiance pour P(x > LSS) sont obtenus à l'aide des formules suivantes :
où
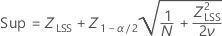
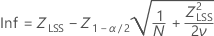
Les intervalles de confiance pour PPM > LSS et % > LSS sont déterminés en multipliant les intervalles de confiance de la probabilité par une constante.
PPM
%
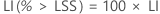
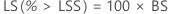
Borne de confiance unilatérale
Pour une borne unilatérale, les calculs sont les suivants :
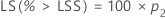
Minitab résout l'équation suivante pour trouver p1 :
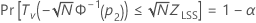
où
Notation
| Terme | Description |
|---|---|
| LSS | limite de spécification supérieure |
| PPM | parties par million |
| LI | borne inférieure |
| LS | borne supérieure |
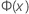 | fonction de répartition (CDF) obtenue avec la loi normale standard |
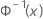 | CDF inverse obtenue avec la loi normale standard |
 | (1 - α/2)ème percentile de la loi normale standard |
| α | alpha du niveau de confiance |
 | moyenne du procédé (estimée à partir des données échantillons ou d'une valeur historique) |
| s | écart type global d'échantillon |
| N | nombre total de mesures |
| υ | degrés de liberté pour s |
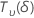 | variable aléatoire distribuée selon une loi t, avec  degrés de liberté et dotée du paramètre de non-centralité δ |
PPM Total pour les performances globales attendues
Le nombre attendu de pièces par million en dehors des limites de spécification, en fonction de la variation globale du procédé, est
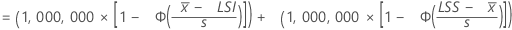
Notation
| Terme | Description |
|---|---|
| PPM | Pièces par million |
| LSI | Limite inférieure de spécification |
| LSS | Limite de spécification supérieure |
| Φ (X) | Fonction de répartition (CDF) d'une loi normale standard |
 | Moyenne des observations |
| s | Ecart type global |
Intervalles de confiance de la valeur PPM totale pour les performances globales attendues lorsque la LSI et la LSS sont toutes les deux connues
La proportion totale de pièces hors spécification, qu'elle soit exprimée en PPM (parties par million) ou en pourcentage, est calculée à partir de la probabilité qu'une pièce se trouve en dehors des limites de spécification.
Intervalles de confiance bilatéraux
Les bornes supérieure et inférieure de l'intervalle de probabilité qu'une pièce soit hors spécification sont calculées à l'aide des fomules suivantes :
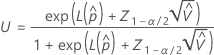
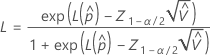
où
Pour calculer 
, remplacez les estimations de l’échantillon par les paramètres de la formule de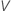 
:
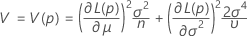
où
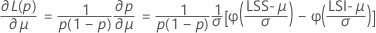
Les bornes de l'intervalle contenant la proportion totale de pièces hors spécification, qu'elle soit exprimée en PPM (parties par million) ou en pourcentage, sont calculées en multipliant les bornes de la probabilité par une constante.
PPM
%
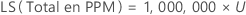
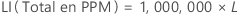
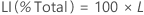
Borne de confiance unilatérale
La borne supérieure de l'intervalle de probabilité qu'une pièce soit hors spécification est calculée à l'aide de la fomule suivante :
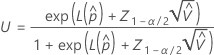
où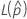 
et 
sont calculés de la même façon que pour l'intervalle bilatéral.
La borne supérieure de l'intervalle contenant la proportion totale de pièces hors spécification en PPM (parties par million) et en pourcentage est déterminée en multipliant la valeur de la borne de la probabilité par une constante.
PPM
%
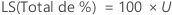
Notation
| Terme | Description |
|---|---|
| LSI | limite de spécification inférieure |
| LSS | limite de spécification supérieure |
| PPM | parties par million |
| LI | borne inférieure |
| LS | borne supérieure |
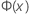 | fonction de répartition (CDF) obtenue avec la loi normale standard |
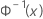 | CDF inverse obtenue avec la loi normale standard |
 | la fonction de densité de probabilité (PDF) à partir d’une distribution normale standard |
 | (1 - α/2)ème percentile de la loi normale standard |
| α | alpha du niveau de confiance |
 | moyenne du procédé (estimée à partir des données échantillons ou d'une valeur historique) |
| s | écart type global d'échantillon |
| N | nombre total de mesures |
| υ | degrés de liberté pour s |
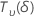 | variable aléatoire distribuée selon une loi t, avec  Degrés de liberté et paramètre de non-centralité δ |
Intervalles de confiance de la valeur PPM totale pour les performances globales attendues dans un procédé incluant une limite de spécification
Pour un procédé n'incluant qu'une limite de spécification inférieure (LSI), l'intervalle de confiance de la proportion totale de pièces PPM hors spécification, exprimée en PPM ou en pourcentage, est identique à celui obtenu pour PPM < LSI ou % < LSI. Reportez-vous à la section PPM < LSI pour les performances globales attendues.
Pour un procédé n'incluant qu'une limite de spécification supérieure (LSS), l'intervalle de confiance de la proportion totale de pièces PPM hors spécification, exprimée en PPM ou en pourcentage, est identique à celui obtenu pour PPM > LSS ou % > LSS. Reportez-vous à la section PPM > LSS pour les performances globales attendues.
