Estimations de MaxV des paramètres de distribution
La méthode du maximum de vraisemblance (ML) estime les valeurs des paramètres de distribution qui maximisent la fonction de vraisemblance pour chaque distribution. L'objectif est d'obtenir le meilleur accord entre le modèle de distribution et les données échantillons observées.
- Emplacement
- Ce paramètre affecte l’emplacement d’une distribution. Par exemple, avec différents paramètres d'emplacement, une loi logistique peut être décalée le long de l'axe horizontal.
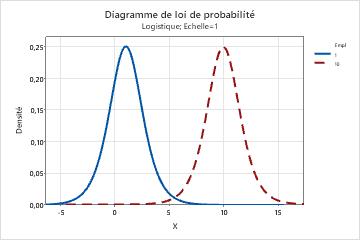
- Forme
- Ce paramètre affecte la forme de la loi de distribution. Par exemple, avec différents paramètres de forme, une loi de Weibull peut sembler plus asymétrique ou plus symétrique.
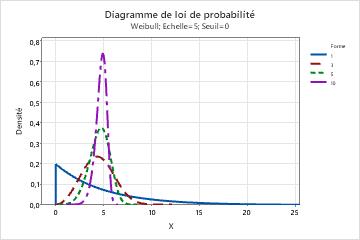
- Echelle
- Ce paramètre affecte l’échelle de la distribution. Par exemple, avec différents paramètres d'échelle, une loi logistique peut sembler plus étirée ou plus comprimée.
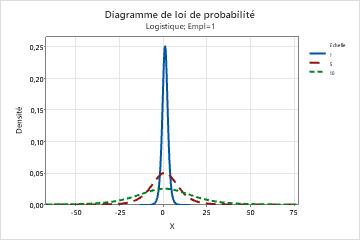
- Seuil
- Ce paramètre affecte la valeur minimale d'une variable aléatoire. Par exemple, avec différents paramètres de seuil, une loi exponentielle peut être définie sur une étendue de valeurs différente.
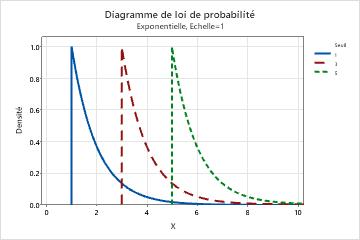
Remarque
Minitab calcule les estimations des paramètres à l'aide de la méthode du maximum de vraisemblance pour toutes les lois à l'exception des lois normales et log-normales, qui utilisent plutôt des estimations de paramètres non biaisées.
Interprétation
Utilisez les estimations de MaxV des paramètres de distribution pour comprendre le modèle de distribution utilisé pour vos données. Par exemple, supposons qu'un ingénieur qualité décide que, à partir des connaissances historiques du procédé et des valeurs de p LRT et d'Anderson-Darling, la loi de Weibull à 3 paramètres offre le meilleur ajustement pour les données de procédé. Pour comprendre la loi de Weibull à 3 paramètres utilisée pour modéliser les données, l'ingénieur examine les estimations de MaxV pour la forme, l'échelle et le seuil calculées pour la loi.
Distribution
L’analyse fournit des statistiques de qualité d’ajustement et des paramètres de distribution pour plusieurs distributions couramment utilisées. Un grand nombre de ces lois sont polyvalentes et peuvent modéliser diverses données continues, y compris des données avec des valeurs positives, négatives et nulles.
- Log-normale
- Exponentielle
- Weibull
- Gamma
- Log-logistique
Ainsi, si vos données contiennent des valeurs négatives ou nulles, Minitab ne présente pas les résultats de ces lois. Dans ce cas, utilisez les résultats de la version avec le plus grand nombre de paramètres de chaque loi. Par exemple, si vos données contiennent des valeurs négatives, Minitab ne communique pas les résultats de la distribution lognormale. Utilisez plutôt les résultats de la loi log-normale à 3 paramètres.
Pour plus d’informations sur les distributions, reportez-vous à la rubrique Pourquoi la loi de Weibull est-elle la loi par défaut pour une analyse de capabilité non normale ?.
Remarque
Pour plus d'informations sur les formules utilisées pour calculer les fonctions PDF et CDF de chaque loi, reportez-vous à la section Méthodes et formules pour les lois de distribution dans Identification de loi individuelle.
P
Remarque
Il n'existe aucune valeur de p pour le test AD disponible pour les lois à 3 paramètres, sauf pour la loi de Weibull.
Interprétation
Utilisez la valeur de p pour évaluer l'ajustement de la loi.
- P ≤ α: Les données ne suivent pas la distribution (Rejet H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et en conclure que vos données ne suivent pas la loi.
- P > α: Impossible de conclure que les données ne suivent pas la distribution (Échec du rejet de H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Il n'existe pas de preuves suffisantes pour conclure que les données ne suivent pas la loi. Vous pouvez supposer que les données suivent la distribution.
- Choisissez la loi la plus couramment utilisée dans votre secteur industriel ou application.
- Choisissez la loi qui fournit les résultats les plus conservateurs. Par exemple, si vous effectuez une analyse de capabilité, vous pouvez le faire à l'aide de différentes lois, puis choisir la loi qui produit les indices de capabilité les plus conservateurs. Pour plus d’informations, allez à Percentiles de loi pour Identification de loi individuelle et cliquez sur « Pourcentages et percentiles ».
- Choisissez la loi la plus simple qui s'ajuste à vos données. Par exemple, si une loi à 2 paramètres et une loi à 3 paramètres fournissent un bon ajustement, vous pouvez choisir la loi plus simple à 2 paramètres.
Important
Soyez prudent lorsque vous interprétez les résultats d’un très petit ou d’un très grand échantillon. Si vous avez un très petit échantillon, un test de qualité d’ajustement peut ne pas avoir assez de puissance pour détecter des écarts significatifs par rapport à la distribution. Si vous avez un très grand échantillon, le test peut être si puissant qu’il détecte même de petits écarts par rapport à la distribution qui n’ont aucune signification pratique. Utilisez les diagrammes de probabilité en plus des valeurs p pour évaluer l’ajustement de la distribution.
Résultats de la distribution automatisée des capacités : Calcium
| Distribution | Emplacement | Echelle | Seuil | Forme | P | Ppk |
|---|---|---|---|---|---|---|
| Normale | 50,7820 | 2,7648 | 0,0463827 | 1,2999 | ||
| Weibull | 52,1368 | 17,825 | <0,01 | 0,7907 | ||
| Log-normale* | 3,9261 | 0,0537 | 0,0848247 | 1,4732 | ||
| Plus petite valeur extrême | 52,2226 | 2,9589 | <0,01 | 0,7153 | ||
| Plus grande valeur extrême | 49,5037 | 2,1699 | >0,25 | |||
| Gamma | 0,1447 | 351,044 | 0,0706812 | 1,4275 | ||
| Logistique | 50,5718 | 1,5948 | 0,0339831 | 1,0023 | ||
| Log-logistique | 3,9226 | 0,0312 | 0,0495201 | 1,0864 | ||
| Exponentielle | 50,7820 | <0,0025 | -0,0378 | |||
| Weibull 3 paramètres | 4,5365 | 46,6658 | 1,476 | >0,5 | ||
| Log-normale à 3 paramètres | 1,6930 | 0,4685 | 44,7401 | |||
| Gamma 3 paramètres | 1,6370 | 45,8838 | 2,992 | |||
| Log-logistique 3 paramètres | 1,5486 | 0,3276 | 45,4618 | |||
| Exponentielle 2 paramètres | 4,0633 | 46,7187 | 0,0140796 | |||
| Transformation de Box-Cox | 0,0000 | 0,0000 | 0,324445 | 2,5062 | ||
| Transformation de Johnson | 0,0290 | 0,9729 | 0,985835 | 2,7129 | ||
| Non paramétrique | 2,8889 |
| Distribution | Cpk |
|---|---|
| Normale | 1,3504 |
| Weibull | |
| Log-normale* | |
| Plus petite valeur extrême | |
| Plus grande valeur extrême | |
| Gamma | |
| Logistique | |
| Log-logistique | |
| Exponentielle | |
| Weibull 3 paramètres | |
| Log-normale à 3 paramètres | |
| Gamma 3 paramètres | |
| Log-logistique 3 paramètres | |
| Exponentielle 2 paramètres | |
| Transformation de Box-Cox | 2,5335 |
| Transformation de Johnson | |
| Non paramétrique |
Dans ces résultats, la distribution log-normale est la première méthode qui ajuste les données au niveau de signification de 0,05. D’autres distributions et transformations fournissent également un ajustement adéquat aux données. Déterminez si l’une de ces méthodes alternatives est plus compatible avec le processus.
Remarque
Pour plusieurs lois de distributions, Minitab affiche également les résultats de la loi avec un paramètre supplémentaire. Par exemple, pour la loi log-normale, Minitab affiche les résultats des versions de la loi à 2 paramètres et 3 paramètres. Pour les distributions qui ont des paramètres supplémentaires, déterminez si le paramètre supplémentaire est compatible avec ce que vous savez du processus. Par exemple, si le processus a une limite physique à une valeur différente de zéro, une distribution avec un paramètre de seuil est compatible avec le processus.
Ppk
- La distance entre la moyenne du procédé et la limite de spécification la plus proche (LSS ou LSI)
- La dispersion unilatérale du procédé (variation de 3 σ), déterminée à partir de sa variation globale
Interprétation
Utilisez Ppk pour évaluer la capabilité globale de votre procédé en fonction de l'emplacement et de la dispersion du procédé. La capabilité globale indique les performances réelles de votre procédé que le client constate au fil du temps.
En règle générale, des valeurs Ppk élevées indiquent que le procédé offre une capabilité satisfaisante. Des valeurs Ppk faibles indiquent que votre procédé peut nécessiter une amélioration.
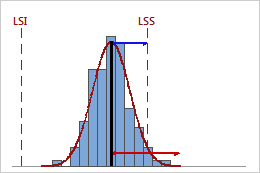
Indice Ppk faible
Dans cet exemple, la distance entre la moyenne du procédé et la limite de spécification la plus proche (LSS) est inférieure à la dispersion unilatérale du procédé. Par conséquent, Ppk est faible (0,66) et la capabilité globale du procédé est insuffisante.
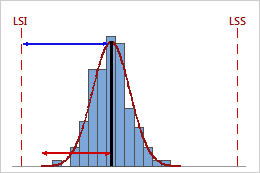
Indice Ppk élevé
Dans cet exemple, la distance entre la moyenne du procédé et la limite de spécification la plus proche (LSI) est supérieure à la dispersion unilatérale du procédé. Par conséquent, Ppk est élevé (1,68) et la capabilité globale du procédé est bonne.
-
Comparez Ppk à une valeur de référence représentant la valeur minimale acceptable pour votre procédé. De nombreux secteurs industriels utilisent une valeur référence de 1,33. Si Ppk est inférieur à votre référence, réfléchissez à des moyens d'améliorer votre procédé.
-
Comparez Pp et Ppk. Si les valeurs de Pp et de Ppk sont à peu près égales, le procédé est centré entre les limites de spécification. Si Pp et Ppk sont différents, le procédé n'est pas centré.
-
Comparez Ppk et Cpk. Lorsqu'un procédé est maîtrisé, Ppk et Cpk sont à peu près égaux. La différence entre les indices Ppk et Cpk représente l'amélioration de la capabilité à laquelle vous pouvez vous attendre si les décalages et les glissements du procédé sont éliminés.
Attention
L'indice Ppk représente uniquement un côté de la courbe du procédé et ne mesure aucunement ses performances de l'autre côté de la courbe.
Par exemple, les graphiques suivants illustrent deux procédés ayant des valeurs Ppk identiques. Toutefois, un procédé enfreint les deux limites de spécification, tandis que l'autre n'enfreint que la limite de spécification supérieure.
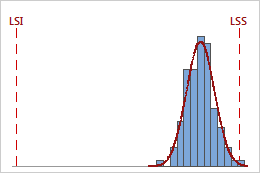
Ppk = min {PPI = 4,01, PPS = 0,64} = 0,64
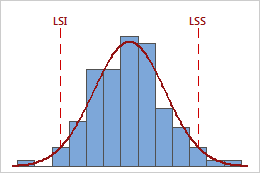
Ppk = PPI = PPS = 0,64
Si votre procédé produit des pièces non conformes qui se situent des deux côtés des limites de spécification, vous pouvez envisager d'utiliser d'autres indices, comme la valeur Z.référence, pour en évaluer la capabilité de façon plus complète.
Cpk
- La distance entre la moyenne du procédé et la limite de spécification la plus proche (LSS ou LSI)
- La dispersion unilatérale du procédé (variation de 3 σ), déterminée à partir de l'écart type à l'intérieur des sous-groupes
Interprétation
Utilisez Cpk pour évaluer la capabilité potentielle de votre procédé en fonction de l'emplacement et de la dispersion du procédé. La capabilité potentielle indique la capabilité pouvant être obtenue si les décalages et les glissements du procédé sont éliminés.
En règle générale, des valeurs Cpk élevées indiquent que le procédé offre une capabilité satisfaisante. Des valeurs Cpk faibles indiquent que votre procédé peut nécessiter une amélioration.
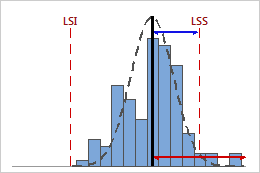
Indice Cpk faible
Dans cet exemple, la distance entre la moyenne du procédé et la limite de spécification la plus proche (LSS) est inférieure à la dispersion unilatérale du procédé. Par conséquent, Cpk est faible (0,80) et la capabilité potentielle du procédé est insuffisante.
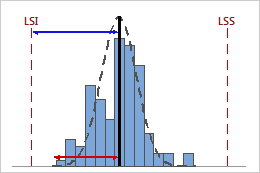
Indice Cpk élevé
Dans cet exemple, la distance entre la moyenne du procédé et la limite de spécification la plus proche (LSI) est supérieure à la dispersion unilatérale du procédé. Par conséquent, Cpk est élevé (1,64) et la capabilité potentielle du procédé est bonne.
Vous pouvez comparer Cpk à d'autres valeurs pour obtenir de plus amples informations sur la capabilité de votre procédé.
-
Comparez Cpk à une valeur de référence représentant la valeur minimale acceptable pour votre procédé. De nombreux secteurs industriels utilisent une valeur référence de 1,33. Si Cpk est inférieur à votre référence, réfléchissez à des moyens d'améliorer votre procédé, par exemple en réduisant sa variation ou en décalant son emplacement.
-
Comparez Cp et Cpk. Si Cp et Cpk sont à peu près égaux, le procédé est centré entre les limites de spécification. Si Cp et Cpk sont différents, le procédé n'est pas centré.
-
Comparez Ppk et Cpk. Lorsqu'un procédé est maîtrisé, Ppk et Cpk sont à peu près égaux. La différence entre les indices Ppk et Cpk représente l'amélioration de la capabilité à laquelle vous pouvez vous attendre si les décalages et les glissements du procédé sont éliminés.
Attention
L'indice Cpk représente uniquement un côté de la courbe du procédé et ne mesure aucunement ses performances de l'autre côté de la courbe.
Par exemple, les graphiques suivants illustrent deux procédés ayant des valeurs de Cpk identiques. Toutefois, un procédé enfreint les deux limites de spécification, tandis que l'autre n'enfreint que la limite de spécification supérieure.
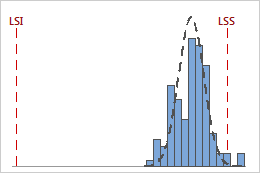
Cpk = min {CPI = 4,58, CPS = 0,93} = 0,93
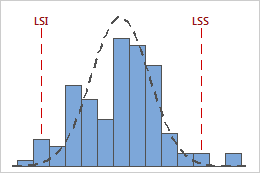
Cpk = CPI = CPS = 0,93
Si votre procédé produit des pièces non conformes qui se situent des deux côtés des limites de spécification, vous pouvez envisager d'utiliser d'autres indices, comme la valeur Z.référence, pour en évaluer la capabilité de façon plus complète.
Cnpk
Cnpk est une mesure de la capabilité globale du processus et est égal au minimum de Cnpu et Cnpl.
- La spécification unilatérale s’étend, de la médiane du processus à la limite supérieure de spécification
- La moitié du processus s’est propagée, de la médiane du processus à l’estimation de l’extrémité supérieure du processus
- La spécification unilatérale s’étend, de la médiane du processus à la limite inférieure de spécification
- La moitié du processus s’est propagée, de la médiane du processus à l’estimation de l’extrémité inférieure du processus
Interprétation
Utilisez Cnpk pour évaluer la capabilité globale de votre processus en fonction de l’emplacement du processus et de l’étendue du processus. La capabilité globale indique les performances réelles de votre procédé que le client constate au fil du temps.
En général, des valeurs Cnpk plus élevées indiquent un processus plus performant. Des valeurs Cnpk plus faibles indiquent que votre processus peut avoir besoin d’amélioration.
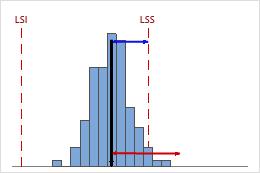
Faible Cnpk
Dans cet exemple, les performances du procédé sont moins bonnes par rapport à sa limite de spécification supérieure que par rapport à sa limite de spécification inférieure. La valeur Cnpk est égale à Cnpu (≈ 0,40), ce qui est faible et indique une faible capabilité.
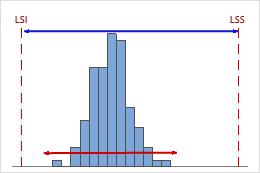
Cnpk élevé
Dans cet exemple, les performances du procédé sont moins bonnes par rapport à sa limite de spécification inférieure que par rapport à sa limite de spécification supérieure. La valeur Cnpk est égale à Cnpl (≈ 1,40), ce qui est élevé et indique une bonne capabilité.
-
Si cnpk < 1,alors la dispersion de spécification est inférieure à la dispersion de processus.
-
Comparez Cnpk à une valeur de référence qui représente la valeur minimale acceptable pour votre processus. De nombreux secteurs industriels utilisent une valeur référence de 1,33. Si Cnpk est inférieur à votre indice de référence, envisagez des moyens d’améliorer votre processus.
Mise en garde
L'indice Cnpk représente uniquement la capabilité du procédé pour le "pire" côté des mesures, c'est-à-dire celui qui présente les moins bonnes performances. Si votre procédé produit des pièces non conformes qui se situent des deux côtés des limites de spécification, consultez les graphiques de capabilité et les probabilités des pièces situées en dehors des deux limites de spécification pour évaluer la capabilité du procédé de façon plus complète.
