Des ingénieurs qualité d'une entreprise fabricant du carrelage étudient les réclamations des clients concernant les déformations des carreaux. Pour assurer la qualité de la production, les ingénieurs mesurent la déformation sur 10 carreaux chaque jour ouvrable pendant 10 jours. La limite de spécification supérieure pour la mesure de déformation est de 6 mm. Les ingénieurs veulent explorer différentes options pour trouver une méthode raisonnable pour estimer la capabilité du processus.
- Ouvrez les données échantillons, DéformationCarreau.MWX.
- Sélectionnez .
- Dans Colonne unique, saisissez Déformation.
- Dans Effectif des sous-groupes, saisissez 10.
- Dans la zone Spécification supérieure, saisissez 6.
- Sélectionnez OK.
Interpréter des résultats
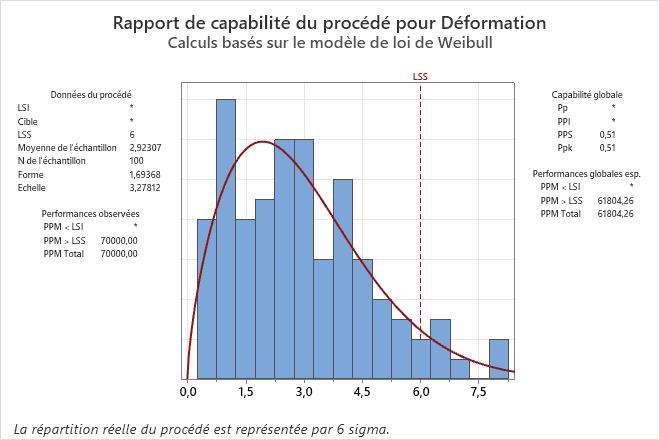
L’analyse affiche un rapport de capabilité pour la première méthode qui fournit un ajustement raisonnable. Pour la déformation des tuiles, les résultats utilisent une distribution de Weibull.
Pour ces données, les mesures sur la queue droite de l’histogramme semblent dépasser la limite supérieure de spécification. Par conséquent, la déformation des carreaux dépasse souvent la limite de spécification supérieure de 6 mm. La valeur PPM > LSS observée indique que 70 000 carreaux sur un million se trouvent au-dessus de la limite de spécification supérieure. L'indice Ppk global est de 0,51, ce qui est inférieur à la valeur de 1,33 généralement acceptée dans le secteur. Par conséquent, les ingénieurs concluent que le procédé ne présente pas une bonne capabilité et ne répond pas aux exigences du client.
Le tableau des résultats de distribution montre l’ordre d’évaluation des méthodes. Dans la première ligne, la conclusion du test d’Anderson-Darling est que les données ne suivent pas une distribution normale au niveau de signification de 0,05 parce que la valeur de p est inférieure à 0,05. Dans la deuxième ligne, la conclusion du test d’Anderson-Darling est que la distribution de Weibull est un ajustement raisonnable aux données parce que la valeur de p est supérieure à 0,05. Les résultats de capabilité sont pour la distribution Weibull parce que la distribution Weibull est la première méthode de la liste qui fournit un ajustement raisonnable.
Les ingénieurs utilisent la connaissance des processus pour déterminer si la distribution de Weibull est une sélection raisonnable. Par exemple, la distribution de Weibull a une frontière à 0. Dans les données, 0 est une limite qui représente une mosaïque non déformée.
Résultats de la distribution automatisée des capacités : Déformation
| Distribution | Emplacement | Echelle | Seuil | Forme | P | Ppk | Cpk |
|---|---|---|---|---|---|---|---|
| Normale | 2,9231 | 1,7860 | 0,0100421 | 0,5743 | 0,5838 | ||
| Weibull* | 3,2781 | 1,6937 | >0,25 | 0,5133 | |||
| Log-normale | 0,8443 | 0,7444 | <0,005 | 0,4242 | |||
| Plus petite valeur extrême | 3,8641 | 1,9924 | <0,01 | 0,5362 | |||
| Plus grande valeur extrême | 2,0958 | 1,4196 | 0,212835 | 0,5130 | |||
| Gamma | 1,2477 | 2,3428 | 0,238337 | 0,4851 | |||
| Logistique | 2,7959 | 1,0162 | 0,0127347 | 0,5799 | |||
| Log-logistique | 0,9097 | 0,4217 | <0,005 | 0,4090 | |||
| Exponentielle | 2,9231 | <0,0025 | 0,3780 | ||||
| Weibull 3 paramètres | 2,9969 | 0,2099 | 1,5049 | 0,467097 | 0,4980 | ||
| Log-normale à 3 paramètres | 1,3788 | 0,4184 | -1,4002 | 0,4961 | |||
| Gamma 3 paramètres | 1,2314 | -0,0197 | 2,3898 | 0,4864 | |||
| Log-logistique 3 paramètres | 1,3043 | 0,2700 | -1,0940 | 0,4656 | |||
| Exponentielle 2 paramètres | 2,6679 | 0,2552 | <0,01 | 0,3982 | |||
| Transformation de Box-Cox | 1,6237 | 0,5380 | 0,574337 | 0,5116 | 0,5214 | ||
| Transformation de Johnson | 0,0112 | 0,9949 | 0,798895 | 0,4959 | |||
| Non paramétrique | 0,6187 |
