Un ingénieur en fabrication a mis en oeuvre un plan d'échantillonnage par mesures pour vérifier l'épaisseur de la paroi d'un tuyau de 2 pouces (entrant). La spécification inférieure pour l'épaisseur des parois de tuyau est de 0,09 pouces. Il est convenu entre l'ingénieur et le fournisseur que le niveau de qualité acceptable (NQA) est de 100 non-conformes par million et que le niveau de qualité rejetable (NQR) est de 300 non-conformes par million. A partir de ces spécifications, l'ingénieur sélectionne et mesure de manière aléatoire 104 tuyaux par lot de 2500. Si la valeur de Z calculée est supérieure à la distance critique (3,55750), l'ingénieur accepte le lot en totalité.
Le chef d'équipe craint que mesurer 104 tuyaux ne prenne trop de temps. Il préfère mesurer moins de tuyaux, par exemple seulement 50. L'ingénieur accepte de comparer différents plans d'échantillonnage pour déterminer les risques et les avantages associés à chacun d'entre eux.
- Sélectionnez .
- Dans la liste déroulante, sélectionnez Comparer les plans d'échantillonnage définis par l'utilisateur.
- Dans Unités des niveaux de qualité, sélectionnez Défectueux pour un million.
- Dans la zone Niveau de qualité acceptable (NQA), saisissez 100.
- Dans la zone Niveau de qualité rejetable (NQR ou LTPD), saisissez 300.
- Dans la zone Effectifs des échantillons, saisissez 50 75 100 104.
- Dans la zone Distances critiques (valeurs k), saisissez 3,55750.
- Dans la zone Spécification inférieure, saisissez 0,09.
- Dans la zone Ecart type historique, saisissez 0,025.
- Dans la zone Taille du lot, saisissez 2500.
- Cliquez sur OK.
Interprétation des résultats
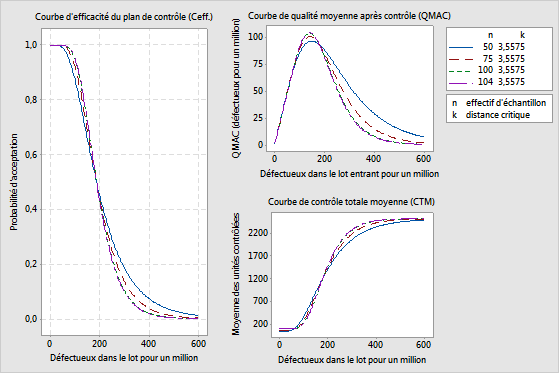
L'ingénieur compare les graphiques des différents plans d'échantillonnage et se rend compte que les plans dont les effectifs d'échantillon sont de 100 et 104 tuyaux sont très similaires. La probabilité d'acceptation aux niveaux NQA et NQR change de moins de 0,5 % (0,95 – 0,947). De même, les valeurs QMAC et CTM changent très peu.
L'ingénieur estime également qu'un effectif d'échantillon de 50 tuyaux ne protège pas assez le niveau de qualité. Avec un effectif d'échantillon de 50, la probabilité d'acceptation d'un lot au NQR (300 PPM) est de 18,7 %. De plus, la probabilité de refuser un lot qui devrait être accepté au NQA (100 PPM) est de 12,7 %, ce qui est trop élevé pour le fournisseur.
L'ingénieur accepte d'évaluer un plan d'échantillonnage avec 75 tuyaux. Les risques en matière de probabilité d'acceptation semblent raisonnables si le fournisseur accepte de réduire la variabilité d'épaisseur des tuyaux. L'ingénieur décide d'évaluer d'autres effectifs d'échantillons, compris entre 75 et 100 tuyaux.
Méthode
| Limite de spécification inférieure (LSI) | 0,09 |
|---|---|
| Ecart type historique | 0,025 |
| Taille du lot | 2500 |
| Niveau de qualité acceptable (NQA) | 100 |
| Niveau de qualité rejetable (NQR ou LTPD) | 300 |
Comparer le(s) plan(s) défini(s) par l'utilisateur
| Effectif d'échantillon(n) | Distance critique(k) | Défectueux pour un million | Probabilité d'acceptation | Probabilité de rejet | QMAC | CTM |
|---|---|---|---|---|---|---|
| 50 | 3,5575 | 100 | 0,873 | 0,127 | 85,6 | 360,4 |
| 50 | 3,5575 | 300 | 0,187 | 0,813 | 54,9 | 2042,6 |
| 75 | 3,5575 | 100 | 0,919 | 0,081 | 89,1 | 271,3 |
| 75 | 3,5575 | 300 | 0,138 | 0,862 | 40,1 | 2165,8 |
| 100 | 3,5575 | 100 | 0,947 | 0,053 | 90,9 | 227,5 |
| 100 | 3,5575 | 300 | 0,104 | 0,896 | 30,0 | 2250,3 |
| 104 | 3,5575 | 100 | 0,950 | 0,050 | 91,1 | 223,2 |
| 104 | 3,5575 | 300 | 0,100 | 0,900 | 28,6 | 2261,3 |
Limites de qualité moyenne après contrôle (LQMAC)
| Effectif d'échantillon | Distance critique(k) | LQMAC | A défectueux pour un million |
|---|---|---|---|
| 50 | 3,5575 | 96,8 | 148,3 |
| 75 | 3,5575 | 101,0 | 141,9 |
| 100 | 3,5575 | 104,2 | 140,1 |
| 104 | 3,5575 | 104,6 | 140,0 |