La distribution d'un échantillonnage décrit la probabilité d'obtenir chaque valeur possible d'une statistique à partir d'un échantillon aléatoire d'une population ; en d'autres termes, la proportion de tous les échantillons aléatoires de cet effectif qui donne cette valeur. Le bootstrap est une méthode d'estimation de la distribution d'échantillonnage fondée sur le prélèvement de plusieurs échantillons avec remise à partir d'un échantillon unique. On appelle ces échantillons répétés des rééchantillonnages. Chaque rééchantillonnage est de la même taille que l'échantillon d'origine.
L'échantillon d'origine représente la population à partir de laquelle il a été prélevé. Les rééchantillonnages provenant de cet échantillon d'origine représentent le résultat que nous obtiendrions si nous prélevions plusieurs échantillons sur cette population. La loi de distribution bootstrap d'une statistique, basée sur les rééchantillonnages, représente la loi de distribution de la statistique.
Par exemple, vous souhaitez estimer la loi de distribution d'échantillonnage de la proportion de M&M's bleus. Vous ouvrez un paquet au hasard et déterminez qu'il y a 102 M&M's, dont 23 (22,5 %) bleus. L'échantillonnage répété avec remise à partir de l'échantillon d'origine illustre ce à quoi la population peut ressembler. Pour effectuer un rééchantillonnage, un M&M est choisi au hasard dans l'échantillon d'origine, sa couleur est enregistrée, et il est remis dans l'échantillon. Cette étape est répétée 102 fois (l'effectif de l'échantillon d'origine) pour réaliser un seul rééchantillonnage. La carte barre suivante représente un seul échantillon bootstrap prélevé sur l'échantillon d'origine.
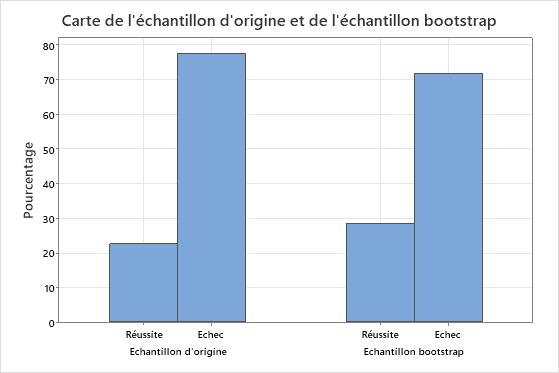
Puisque le rééchantillonnage est obtenu par un échantillonnage avec remise, la proportion d'échantillon bootstrap ne sera généralement pas exactement la même que la proportion d'origine. Cette carte barre montre qu'environ 22,5 % des M&M's de l'échantillon d'origine étaient bleus, contre 28,4 % pour l'échantillon bootstrap. Pour créer une loi de distribution bootstrap, vous devez effectuer de nombreux rééchantillonnages. L'histogramme suivant montre la distribution bootstrap pour 1 000 rééchantillonnages pour le paquet de M&M's d'origine.
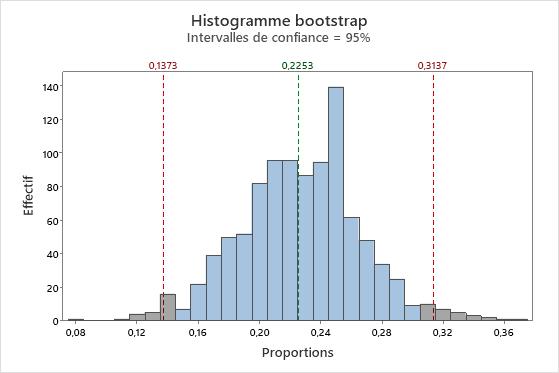
La distribution bootstrap est centrée sur environ 22,5 %, ce qui représente une estimation de la proportion de la population. Les lignes de référence rouges représentent un intervalle de confiance à 95 %. 95 % des valeurs du milieu de la distribution bootstrap fournissent donc un intervalle de confiance à 95 % pour le paramètre. Dans cet exemple, vous pouvez être sûr à 95 % que la proportion de la population de M&M's bleus se situe environ entre 13,7 % et 31,4 %.
Techniques de bootstrap et théorème central limite
Le théorème central limite est un théorème fondamental du domaine de la probabilité et des statistiques. Le théorème affirme que la loi de 
, qui est la moyenne d'un échantillon aléatoire d'une population avec une variance finie, est à peu près distribuée normalement lorsque l'effectif de l'échantillon est élevé, indépendamment de la forme de la distribution de la population. Les techniques de bootstrap peuvent être utilisées pour facilement comprendre le fonctionnement du théorème central limite. Prenez les données issues d'une loi exponentielle.
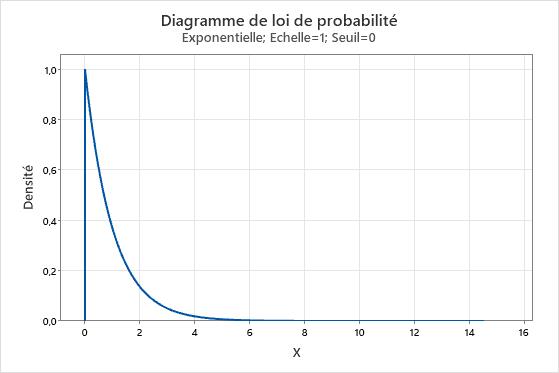
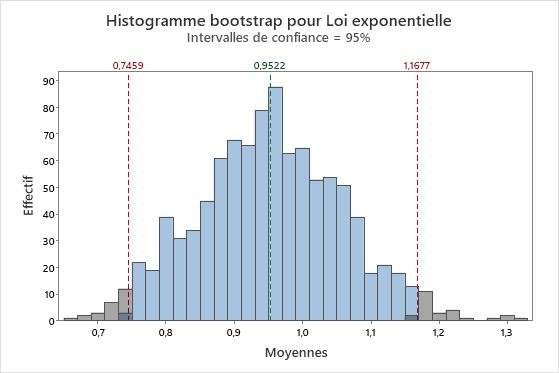
Il est évident que les données sont anormales. Mais nous allons à présent prélever un échantillon de 50 observations et créer une distribution bootstrap des moyennes de 10 rééchantillonnages.
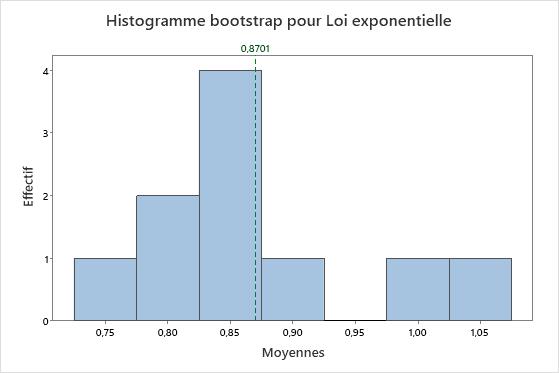
La loi de distribution des moyennes est très différente de la loi exponentielle. Elle ressemble beaucoup plus à une loi normale. Cette ressemblance augmente avec le nombre de rééchantillonnages. Avec 1 000 rééchantillonnages, la loi de distribution de la moyenne des rééchantillonnages est approximativement normale.
