Qu'est-ce que la loi de Poisson ?
La loi de Poisson est caractérisée par un seul paramètre, lambda (λ). Ce paramètre représente la moyenne et la variance. Si lambda est suffisamment élevé, la loi normale (λ, λ) peut être utilisée pour obtenir une approximation de la loi de Poisson.
Utilisez la loi de Poisson pour décrire le nombre d'occurrences d'un événement dans un espace d'observation fini. Par exemple, une loi de Poisson peut indiquer le nombre de défauts dans le système mécanique d'un avion ou le nombre d'appels émis vers un centre d'appels en une heure. La loi de Poisson est souvent utilisée dans le contrôle de la qualité, les études de fiabilité/survie et les assurances.
- Les données sont des dénombrements d'événements (entiers non négatifs sans borne supérieure).
- Tous les événements sont indépendants.
- Le taux moyen ne change pas au cours de la période analysée.
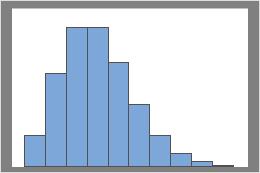
Lambda = 3
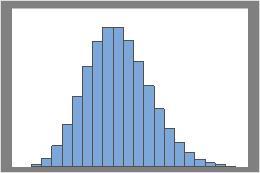
Lambda = 10
Qu'est-ce que le taux d'occurrence ?
Le taux d'occurrence est égal à la moyenne (λ) divisée par la dimension de votre espace d'observation. Elle est utile pour comparer les dénombrements des données de Poisson dans différents espaces d'observation. Par exemple, le standard A reçoit 50 appels téléphoniques en 5 heures et le standard B en reçoit 80 en 10 heures. Vous ne pouvez pas comparer ces valeurs directement car leurs espaces d'observation sont différents. Vous devez calculer le taux d'occurrence pour comparer ces dénombrements. Le taux du standard A est de (50 appels/5 heures) = 10 appels par heure. Le taux du standard B est de (80 appels/10 heures) = 8 appels par heure.
Différences entre la loi de Poisson et la loi binomiale
La loi de Poisson est semblable à la loi binomiale, car toutes deux modélisent des dénombrements d'événements. Toutefois, la loi de Poisson ne place aucune borne supérieure sur ce dénombrement dans la limite de son espace d'observation fini : un standard peut recevoir un nombre infini d'appels en une journée et ne pas aller à l'encontre des exigences de la loi de Poisson. A l'inverse, la loi binomiale définit une limite supérieure sur le dénombrement : le nombre d'événements observés ne peut pas être supérieur au nombre d'essais réalisés.
