Utilisez la loi exponentielle pour modéliser le temps écoulé entre des événements dans un procédé de Poisson continu. Nous considérons que les événements indépendants surviennent à une fréquence constante.
Cette loi a une multitude d'applications, dont les analyses de fiabilité des produits et des systèmes, la théorie des files d'attente et les chaînes de Markov.
- Le temps avant défaillance de composants électroniques
- L'intervalle de temps entre les arrivées des clients à un guichet
- Le temps avant que les clients de la file d'attente ne soient servis
- Le temps avant un défaut de paiement (modélisation du risque de crédit)
- Le temps de demie-vie d'une substance radioactive
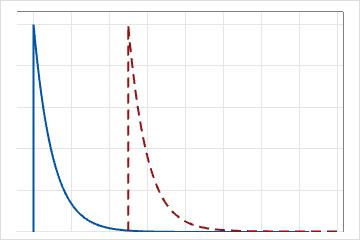
Pour la loi exponentielle à 1 paramètre, le seuil est de zéro et la loi est définie par son paramètre d'échelle. Pour la loi exponentielle à 1 paramètre, le paramètre d'échelle est égal à la moyenne.
Que signifie l'absence de mémoire ?
La loi exponentielle se caractérise essentiellement par son absence de mémoire. La probabilité d'occurrence d'un événement ne dépend pas des essais précédents. De ce fait, le taux d'occurrence reste constant.
Cette absence de mémoire indique que la durée de vie restante d'un composant ne dépend pas de l'âge qu'il a actuellement. Une série de lancers de pièce aléatoires est un exemple d'essais avec absence de mémoire. Un système exposé à une usure normale et qui présente de ce fait un plus grand risque de défaillances pour la suite n'est pas sans mémoire.
