Vous pouvez calculer les valeurs des fonctions de densité de probabilité, les fonctions de répartition ou l'inverse des fonctions de répartition de vos données, pour la loi de distribution sélectionnée dans le menu.
- Fonction d'une loi de probabilité (PDF)
- La fonction d'une loi de probabilité (PDF) définit des zones de forte et de faible probabilité pour les valeurs d'une variable aléatoire. Par exemple, pour une loi normale, la valeur PDF la plus élevée se trouve au niveau de la moyenne, alors que les valeurs PDF les moins élevées se trouvent aux extrémités.
- Fonction de répartition (CDF)
- La fonction de répartition (CDF) calcule la probabilité cumulée jusqu'à la valeur variable que vous indiquez. Utilisez la CDF pour déterminer la probabilité qu'une observation aléatoire extraite de la population soit inférieure ou égale à une certaine valeur. Par exemple, une fonction de répartition peut indiquer la proportion d'arbres dans une forêt dont le diamètre est de 25 centimètres ou moins.
- Fonction de répartition inverse (CDF inverse)
- La fonction de répartition inverse (CDF inverse) indique la valeur de variable associée à une probabilité cumulée spécifique. Par exemple, un ingénieur fiabiliste souhaite déterminer la durée au bout de laquelle des proportions spécifiques de composants tombent en panne. Il peut utiliser la CDF inverse pour déterminer le 95e percentile de la loi de distribution des moments de défaillance.
Exemples pour les loi continues
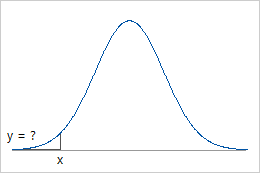
Utilisez la fonction PDF si vous connaissez x et que vous voulez obtenir la valeur de y correspondante sur la courbe.
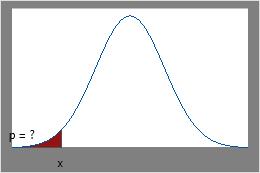
CDF
Utilisez la fonction CDF si vous connaissez x et que vous voulez obtenir l'aire sous la courbe.
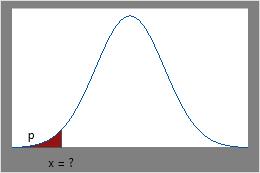
CDF inverse
Utilisez la CDF inverse si vous connaissez l'aire cumulée sous la courbe et que vous voulez obtenir la valeur de x.
