Exemple d'utilisation de la fonction de répartition inverse permettant de déterminer les périodes de garantie
Par exemple, un fabricant d’appareils examine les temps de défaillance de l’élément chauffant dans ses grille-pains. Ils veulent déterminer à quel moment certaines proportions d’éléments chauffants vont céder afin de pouvoir définir la période de garantie. Les temps de défaillance des éléments chauffants suivent une distribution normale avec une moyenne de 1000 heures et un écart-type de 300 heures. La fonction de densité de probabilité (PDF) aide à identifier les régions où les probabilités de défaillance sont plus élevées et plus faibles. L’inverse de la CDF donne le temps de défaillance correspondant pour chaque probabilité cumulative.
Utilisez l’inverse de la CDF pour estimer le temps pendant lequel 5 % des éléments chauffants vont céder, les temps intermédiaires entre lesquels 95 % de tous les éléments chauffants lâcheront, ou le temps où seulement 5 % des éléments chauffants restent. L’inverse de la CDF pour des probabilités cumulatives spécifiques est égal au temps de défaillance sur le côté droit de la zone ombrée sous la courbe PDF.
Déterminez à quel moment 5 % échoueront
- Sélectionnez .
- Choisissez Probabilité cumulée inverse. Dans Moyenne, entrez 1000. Dans Ecart type, entrez 300. Dans Constante d'entrée, entrez 0,05.
- Cliquez sur OK.
Le temps auquel 5 % des éléments chauffants devraient avoir lâché est l’inverse du CDF de 0,05 ou 506,544 heures.
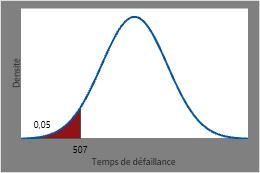
Ce diagramme présente la CDF inverse.
Déterminez les moments entre lesquels 95 % échoueront
- Sélectionnez .
- Choisissez Probabilité cumulée inverse. Dans Moyenne, entrez 1000. Dans Ecart type, entrez 300. Dans Constante d'entrée, entrez 0,025. Cliquez sur OK.
Le temps auquel 2,5 % des éléments chauffants devraient avoir lâché est l’inverse du CDF de 0,025 ou 412 heures.
- Répétez l’étape 2, mais entrez 0,975 au lieu de 0,025. Cliquez sur OK.Le temps auquel 97,5 % des éléments chauffants devraient avoir lâché est l’inverse du CDF de 0,975 ou 1588 heures.
Ainsi, les temps entre lesquels 95 % de tous les éléments chauffants devraient céder correspondent à l’inverse de la CDF de 0,025 et l’inverse de la CDF de 0,975, soit 412 heures et 1588 heures.
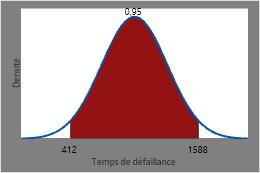
Ce diagramme présente la CDF inverse.
Déterminez à quel moment 5 % survivront
- Sélectionnez .
- Choisissez Probabilité cumulée inverse. Dans Moyenne, entrez 1000. Dans Ecart type, entrez 300. Dans Constante d'entrée, entrez 0,95.
- Cliquez sur OK.
Le temps auquel seuls 5 % des éléments chauffants sont censés rester est l’inverse du CDF de 0,95 ou 1493 heures.
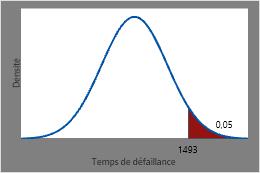
Ce diagramme présente la CDF inverse.
Exemple d’utilisation de la CDF et de l’ICDF avec la distribution hypergéométrique
Lorsque vous essayez de déterminer la probabilité cumulative inverse d’une distribution discrète, la sortie dans contient deux ensembles de colonnes.
Supposons que vous ayez la probabilité cumulative inverse d’une proportion, p. Le premier ensemble de colonnes dans la sortie liste le plus grand x tel que P(X ≤ x) ≤ p. Le second ensemble de colonnes liste le plus petit x tel que P(X ≤ x) ≥ p.
Calculer la probabilité cumulative d’une distribution hypergéométrique
- Dans la feuille de calcul colonne C1, entrez 0 1 2.
C1 0 1 2 - Sélectionnez .
- Choisissez Probabilité cumulée.
- Dans Effectif de la population (N), tape 20000.
- Dans Nombre d'événements de la population (M), tape 2000.
- Dans Effectif d'échantillon (n), tape 20.
- Choisissez Colonne d'entrée et entrez C1. Cliquez sur OK.
Fonction de répartition
- P(X ≤ 0) = 0,121448. La probabilité de ne pas avoir de défaut est d’environ 12 %.
- P(X ≤ 1) = 0,391619. La probabilité d’avoir 0 ou 1 défaut est d’environ 39 %.
- P(X ≤ 2) = 0,676941. La probabilité d’avoir 0, 1 ou 2 défauts est d’environ 68 %.
Calculer la probabilité cumulative inverse d’une distribution hypergéométrique
Maintenant que vous connaissez les probabilités cumulées associées au nombre de défauts, calculez l’inverse de la probabilité cumulative.
Supposons que vous vouliez calculer le nombre de défauts, x, tel que la probabilité cumulative, p, soit de 0,50. Grâce aux résultats précédents, vous savez que P(X ≤ 1) = 0,391619 et que P(X ≤ 2) = 0,676941. Parce que la distribution hypergéométrique est une distribution discrète, le nombre de défauts ne peut pas être compris entre 1 et 2. En d’autres termes, vous pouvez avoir 1 ou 2 défauts, mais pas 1,4 défaut. Ainsi, si vous choisissez Constante d'entrée et entrez 0,50, Minitab calcule les deux probabilités dans la sortie, comme montré dans l’exemple suivant :
- Sélectionnez .
- Choisissez Probabilité cumulée inverse.
- Dans Effectif de la population (N), tape 20000.
- Dans Nombre d'événements de la population (M), tape 2000.
- Dans Effectif d'échantillon (n), tape 20.
- Choisissez Constante d'entrée, et tapez 0,50. Cliquez sur OK.
Fonction de répartition inverse
La première probabilité indique une valeur de x pour laquelle P(X ≤ x) < p, et la deuxième probabilité indique la plus petite valeur de x pour laquelle P(X ≤ x) ≥ p. Dans cet exemple, la première probabilité montre le nombre le plus élevé de défectueux (x = 2), pour lequel P(X ≤ 2) < 0,5, et la<1 id="127">2e</1> probabilité montre le nombre le plus faible de défectueux (x = 3) pour lequel P(X ≤ 3) ≥ 0,5.
Utiliser l’ICDF pour calculer les valeurs critiques
Vous pouvez utiliser Minitab pour calculer une valeur critique pour un test d’hypothèse au lieu de consulter un tableau.
Supposons que vous réalisiez un test du chi-carré avec un α = 0,02 et 12 degrés de liberté. Quelle est la valeur critique correspondante ? Un α = 0,02 correspond à une probabilité cumulative de 1 – 0,02 = 0,98.
- Sélectionnez .
- Choisissez Probabilité cumulée inverse.
- Dans Degrés de liberté, entrez 12.
- Choisissez Constante d'entrée et entrez 0,98.
- Cliquez sur OK.
Minitab affiche la valeur critique, 24,054. Pour le test du chi carré, si la statistique du test est supérieure à la valeur critique, on peut conclure qu’il existe des preuves statistiques pour rejeter l’hypothèse nulle.
Remarque
Cet exemple utilise la distribution du chi carré. Cependant, vous suivez ces mêmes étapes pour toute distribution que vous choisissez.
