Exemple d’utilisation du CDF pour évaluer les poids de remplissage
Par exemple, les poids des boissons gazeuses peuvent remplir suivent une distribution normale avec une moyenne de 12 onces et un écart-type de 0,25 once. La fonction de densité de probabilité (PDF) décrit la probabilité des valeurs possibles du poids de remplissage. La CDF fournit la probabilité cumulative pour chaque valeur x.
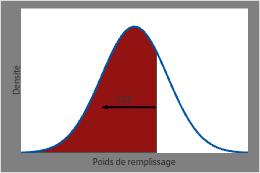
Le CDF pour les poids de remplissage en un point précis est égal à la zone ombragée sous la courbe PDF à gauche de ce point.
Utilisez le CDF pour déterminer la probabilité qu’une canette de soda choisie au hasard ait un poids de remplissage inférieur à 11,5 onces, supérieur à 12,5 onces, ou entre 11,5 et 12,5 onces.
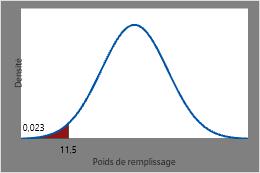
La probabilité qu’une canette de soda choisie au hasard ait un poids de remplissage inférieur ou égal à 11,5 onces est la CDF à 11,5, soit environ 0,023.
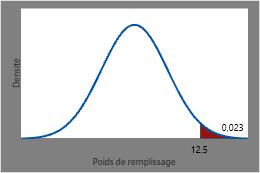
La probabilité qu’une canette de soda choisie au hasard ait un poids de remplissage supérieur à 12,5 onces est de 1 moins le CDF à 12,5 (0,977), soit environ 0,023.
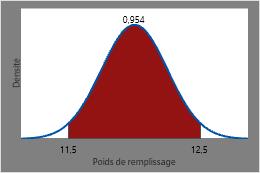
La probabilité qu’une canette de soda choisie au hasard ait un poids de remplissage entre 11,5 onces et 12,5 onces est la CDF à 12,5 moins la CDF à 11,5, soit environ 0,954.
Utilisez le CDF pour calculer les valeurs p
Pour calculer une valeur p pour un test F, vous devez d’abord calculer la fonction de distribution cumulative (CDF). La valeur p est 1 – CDF.
Supposons que vous réalisiez une analyse de régression linéaire multiple avec les degrés de liberté suivants : DF (Régression) = 3, DF (Erreur) = 25 et - statistique F = 2,44.
Calculer une valeur p pour le test F
- Sélectionnez .
- Choisissez Probabilité cumulée.
- Dans Paramètre de non-centralité, entrez 0.
- Dans Degrés de liberté du numérateur, entrez 3.
- Dans Degrés de liberté du dénominateur, entrez 25.
- Choisissez Constante d'entrée et saisissez 2.44.
- Dans la zone Stockage facultatif, saisissez K1. Cliquez sur OK. K1 contient la fonction de distribution cumulative.
Utilisez la calculatrice pour soustraire la valeur p de 1
- Choisissez .
- Dans Stocker le résultat dans la variable, entre la valeur P.
- Dans la zone Expression, saisissez 1-K1. Cliquez sur OK.
Remarque
Cet exemple concerne une distribution F ; Cependant, vous pouvez utiliser une méthode similaire pour d’autres distributions.
