Qu'est ce qu'une loi de distribution continue ?
Une loi continue décrit les probabilités des valeurs possibles d'une variable aléatoire continue. Une variable aléatoire continue est une variable aléatoire qui possède un ensemble de valeurs possibles (appelé étendue) infini et non dénombrable.
Les probabilités d'une variable aléatoire continue (X) sont définies par l'aire de la zone située sous la courbe de sa fonction PDF. Aussi, seules les étendues de valeurs peuvent avoir une probabilité différente de zéro. La probabilité qu'une variable aléatoire continue soit égale à une certaine valeur est toujours égale à zéro.
Exemple de loi de distribution de poids
La loi normale continue peut décrire la distribution du poids d'adultes de sexe masculin. Par exemple, vous pouvez calculer la probabilité qu'un homme pèse entre 72 et 77 kg.
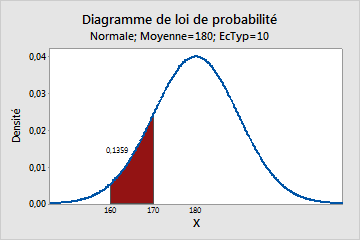
Diagramme de répartition du poids d'adultes de sexe masculin
Dans cet exemple, la zone en couleur sous la courbe représente l'étendue située entre 160 et 170 livres (72 - 77 kg). L'aire correspondant à cette étendue est égale à 0,136 ; par conséquent, la probabilité qu'un homme sélectionné au hasard pèse entre 72 et 77 kg est de 13,6 %. La totalité de l'aire de la zone située sous la courbe est égale à 1,0.
En revanche, la probabilité que la variable X soit exactement égale à une certaine valeur est toujours égale à zéro, car l'aire sous la courbe à un point donné, qui ne présente aucune largeur, est égale à zéro. Par exemple, la probabilité qu'un homme pèse exactement 86 kg, avec une précision absolue, est égale à zéro. Vous pouvez calculer une probabilité différente de zéro selon laquelle un homme pèse plus de 86 kg, moins de 86 kg ou entre 85,9 et 86,1 kg, mais la probabilité qu'il pèse exactement 86 kg est égale à zéro.
Qu'est-ce qu'une loi de probabilité discrète ?
Une loi de probabilité discrète décrit la probabilité d'occurrence de chaque valeur d'une variable aléatoire discrète. Une variable aléatoire discrète est une variable aléatoire comportant des valeurs dénombrables, telles qu'une liste d'entiers non négatifs.
Avec une loi de probabilité discrète, chaque valeur possible de la variable aléatoire discrète peut être associée à une probabilité non nulle. Aussi, une loi de probabilité discrète est souvent présentée sous la forme d'un tableau.
Exemple sur le nombre de plaintes de clients
| x | P (X = x) |
|---|---|
| 5 | 0,037833 |
| 10 | 0,12511 |
| 15 | 0,034718 |
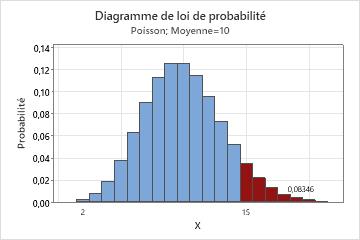
Diagramme de répartition représentant le nombre de plaintes de clients
Dans cet exemple, les barres colorées représentent le nombre d'occurrences où le nombre de plaintes de clients est de 15 par jour ou plus. La somme de la hauteur des barres s'élève à 0,08346. Ainsi, la probabilité que le nombre d'appels par jour soit d'au moins 15 est de 8,35 %.
