Sur ce thème
Histogramme
Un histogramme divise les valeurs des échantillons en plusieurs intervalles et représente l'effectif des valeurs contenues dans chaque intervalle par une barre.
Interprétation
50 rééchantillonnages
1 000 rééchantillonnages
La loi de distribution est généralement plus facile à déterminer avec davantage de rééchantillonnages. Par exemple, dans ces données, la loi de distribution est ambiguë pour 50 rééchantillonnages. Avec 1 000 rééchantillonnages, la forme est approximativement normale.
L'histogramme permet de visualiser les résultats du test de l'hypothèse. Les échantillons de randomisation représentent ce à quoi un échantillon aléatoire ressemblerait si les moyennes de population étaient égales, et l'histogramme est donc centré autour de 0. Pour un test unilatéral, une ligne de référence est tracée au niveau de la différence entre les moyennes des échantillons d'origine. Pour un test bilatéral, une ligne de référence est tracée au niveau de la différence entre les moyennes des échantillons d'origine et à la même distance de l'autre côté de 0. La valeur de p est la proportion des différences issues de rééchantillonnages qui sont plus extrêmes que les valeurs auxquelles sont tracées les lignes de référence. En d'autres termes, la valeur de p est la proportion des différences issues des rééchantillonnages qui sont aussi extrêmes que celle entre vos échantillons d'origine lorsque que vous supposez que l'hypothèse nulle est vraie. Ces différences apparaissent en rouge sur l'histogramme.
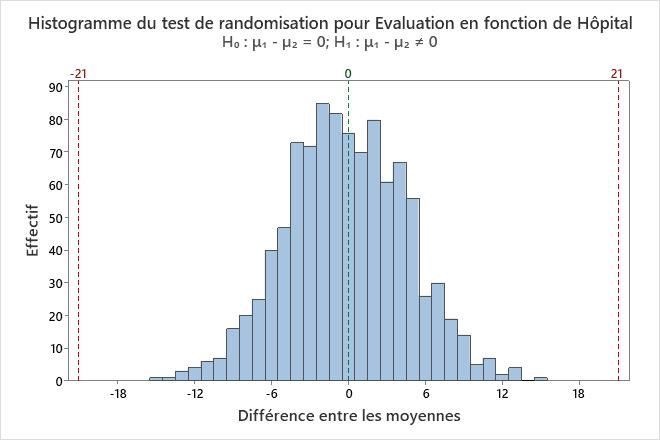
Sur cet histogramme, la distribution bootstrap semble normale. Aucune des différences issues des rééchantillonnages n'est supérieure à 21 ou inférieure à -21.
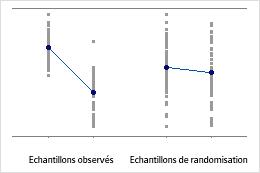
Diagramme des valeurs individuelles
Un diagramme des valeurs individuelles présente les valeurs individuelles contenues dans l'échantillon. Chaque cercle représente une observation. Un diagramme des valeurs individuelles est particulièrement utile lorsque vous disposez de relativement peu d'observations et que vous avez besoin d'évaluer l'effet de chacune d'entre elles.
Remarque
Minitab affiche un diagramme des valeurs individuelles uniquement lorsque vous n'effectuez qu'un seul rééchantillonnage. Minitab affiche à la fois les données d'origine et celles du rééchantillonnage.
Interprétation
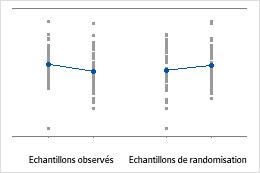
Les moyennes de population sont égales
La moyenne de population du groupe 1 est deux fois plus importante que celle du groupe 2
Hypothèse nulle et hypothèse alternative
- Hypothèse nulle
- L'hypothèse nulle affirme qu'un paramètre de la population (la moyenne, l'écart type, etc.) est égal à une valeur hypothétisée. L'hypothèse nulle est souvent une déclaration initiale basée sur des analyses précédentes ou des connaissances spécialisées.
- Hypothèse alternative
- L'hypothèse alternative affirme qu'un paramètre de la population est plus petit, plus grand ou différent de la valeur hypothétisée dans l'hypothèse nulle. L'hypothèse alternative est celle que vous pensez être vraie ou que vous espérez démontrer.
Méthode
| μ₁ : moyenne de population de Evaluation lorsque Hôpital = A |
|---|
| µ₂ : moyenne de population de Evaluation lorsque Hôpital = B |
| Différence : μ₁ - µ₂ |
Echantillons observés
| Hôpital | N | Moyenne | EcTyp | Variance | Minimum | Médiane | Maximum |
|---|---|---|---|---|---|---|---|
| A | 20 | 80,30 | 8,18 | 66,96 | 62,00 | 79,00 | 98,00 |
| B | 20 | 59,30 | 12,43 | 154,54 | 35,00 | 58,50 | 89,00 |
Différence entre les moyennes observées
| Moyenne de A - Moyenne de B = 21,000 |
|---|
Test de randomisation
| Hypothèse nulle | H₀ : μ₁ - µ₂ = 0 |
|---|---|
| Hypothèse alternative | H₁ : μ₁ - µ₂ ≠ 0 |
| Nombre de rééchantillonnages | Moyenne | EcTyp | Valeur de P |
|---|---|---|---|
| 1000 | -0,185 | 4,728 | < 0,002 |
Dans ces résultats, l'hypothèse nulle est la suivante : la différence de la population est égale à 0. L'hypothèse alternative stipule quant à elle que la différence n'est pas égale à 0.
Nombre de rééchantillonnages
Le nombre de rééchantillonnages est le nombre de fois que Minitab prélève un échantillon aléatoire avec remise dans votre ensemble de données d'origine. Généralement, un grand nombre de rééchantillonnages donne de meilleurs résultats. L'effectif d'échantillon pour chaque rééchantillonnage est égal à l'effectif d'échantillon de l'ensemble de données d'origine. Le nombre de rééchantillonnages est égal au nombre d'observations dans l'histogramme.
Moyenne
La moyenne est la somme de toutes les différences entre les moyennes des échantillons de randomisation divisée par le nombre de rééchantillonnages. Minitab présente deux valeurs différentes pour la différence entre les moyennes : la différence entre les échantillons observés et la différence moyenne entre les échantillons de bootstrap. Ces deux valeurs sont une estimation de la différence entre les moyennes de population et sont généralement similaires. En cas de différence importante entre ces deux valeurs, augmentez l'effectif de vos échantillons d'origine.
EcTyp (échantillon bootstrap)
L'écart type est la mesure la plus courante de la dispersion ou de la répartition des données sur la moyenne. Le symbole σ (sigma) est souvent utilisé pour représenter l'écart type d'une population, tandis que s sert à représenter l'écart type d'un échantillon. Une variation qui est aléatoire ou naturelle pour un procédé est souvent appelée un bruit. Etant donné que l'écart type utilise les mêmes unités que les données, il est généralement plus facile à interpréter que la variance.
L'écart type des échantillons bootstrap (également appelé erreur type bootstrap) est une estimation de l'écart type de la loi d'échantillonnage de la différence entre les moyennes.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des différences issues des rééchantillonnages choisies par rapport à la moyenne globale des différences. Plus l'écart type est élevé, plus les différences sont dispersées. D'une manière générale, pour une loi normale, environ 68 % des valeurs se situent à moins d'un écart type de la moyenne globale des différences, 95 % des valeurs se situent à moins de deux écarts types et 99,7 % des valeurs se situent à moins de trois écarts types.
Utilisez l'erreur type des échantillons bootstrap pour déterminer avec quelle précision les différences issues des rééchantillonnages permettent d'estimer la différence entre les moyennes de population. Plus la valeur est faible, plus l'estimation de la différence de population est précise. En règle générale, plus l'écart type est grand, plus l'erreur type bootstrap sera élevée et moins l'estimation de la différence de population sera précise. En revanche, plus l'effectif d'échantillon est élevé, plus l'erreur type bootstrap de la différence sera faible et plus l'estimation de la différence de population sera précise.
Valeur de p
La valeur de p est la proportion des différences issues des rééchantillonnages qui sont aussi extrêmes que celle entre vos échantillons d'origine lorsque que vous supposez que l'hypothèse nulle est vraie. Une valeur de p inférieure permet d'invalider l'hypothèse nulle avec plus de certitude.
Interprétation
- Valeur de p ≤ α : la différence entre les moyennes est statistiquement significative (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous rejetez l'hypothèse nulle. Vous pouvez conclure que la différence entre les moyennes de population est statistiquement significative. Pour calculer un intervalle de confiance et déterminer si la différence est significative dans la pratique, utilisez la fonction Techniques de bootstrap pour les moyennes de 2 échantillons. Pour plus d'informations, reportez-vous à la rubrique Signification statistique et pratique.
- Valeur de p > α : la différence entre les moyennes n'est pas statistiquement significative (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle. Vous n'êtes pas en mesure de conclure que la différence entre les moyennes de population est statistiquement significative.
