Assistance de Minitab® 

Sélectionner la loi et saisir les paramètres

En savoir plus sur Minitab
Choisissez Calc > Données aléatoires, sélectionnez la loi, puis saisissez les paramètres.

Sur ce thème

Bernoulli

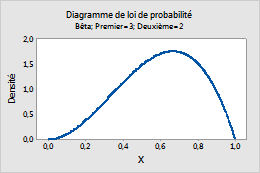
Dans la zone Probabilité d'événement, saisissez une valeur comprise entre 0 et 1 représentant la probabilité que le résultat qui vous intéresse se produise. Une occurrence est appelée "événement". Pour plus d'informations, reportez-vous à la rubrique Loi de Bernoulli.
Utilisez la loi de Bernoulli lorsqu'un procédé aléatoire a exactement deux résultats : événement ou non-événement. Des suites d'essais de Bernoulli indépendants génèrent les autres lois, comme la loi bionmiale, qui modélise le nombre de succès sur n essais. Par exemple, ce diagramme présente un échantillon aléatoire obéissant à une loi binomiale comportant 1 essai et une probabilité d'événement de 0,15.

Bêta

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi bêta.

  1. Dans la zone Premier paramètre de forme, saisissez un nombre positif pour le premier paramètre de forme.
  2. Dans la zone Deuxième paramètre de forme, saisissez un nombre positif pour le deuxième paramètre de forme.

Par exemple, ce diagramme représente une loi bêta disposant d'une première forme de 3 et d'une deuxième forme de 2.

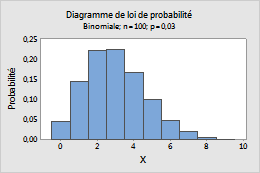
Binomiale

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi binomiale.

  1. Dans la zone Nombre d'essais, entrez l'effectif d'échantillon.
  2. Dans la zone Probabilité d'événement, saisissez une valeur comprise entre 0 et 1 représentant la probabilité que le résultat qui vous intéresse se produise. Une occurrence est appelée "événement".

Par exemple, ce diagramme représente une loi binomiale comportant 100 essais et une probabilité d'événement de 0,03.

Cauchy

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi de Cauchy.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi de distribution.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi de distribution.

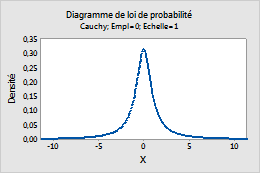
Par exemple, ce diagramme représente une loi de Cauchy dont l'emplacement est de 0 et l'échelle de 1.

Khi deux

Dans Degrés de liberté, saisissez le nombre de degrés de liberté définissant la Loi du Khi deux.

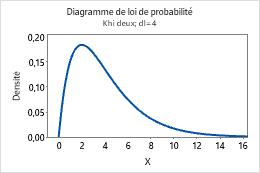
Par exemple, ce diagramme présente une loi du Khi deux ayant 4 degrés de liberté.

Discrète

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi de probabilité discrète.

  1. Dans la zone Valeurs dans, saisissez la colonne qui contient les valeurs à inclure dans la loi. Les valeurs sont habituellement des dénombrements ou des événements discrets qui sont représentés par des valeurs numériques.
  2. Dans la zone Probabilités dans, saisissez la colonne qui contient les probabilités pour chaque valeur. Les probabilités doivent être comprises entre 0 et 1 et leur somme doit être égale à 1.

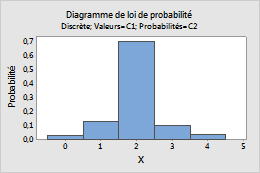
Dans cette feuille de travail, la colonne Valeur contient les dénombrements à inclure dans la loi et la colonne Probabilité contient la probabilité de chaque dénombrement.

C1 C2
Valeur Probabilité
0 0,03
1 0,13
2 0,70
3 0,10
4 0,04

Exponentielle

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi exponentielle.

  1. Dans la zone Echelle, saisissez le paramètre d'échelle. Le paramètre d'échelle est égal à la moyenne lorsque le paramètre de seuil est égal à 0.
  2. Dans la zone Seuil, saisissez la borne inférieure de la loi.

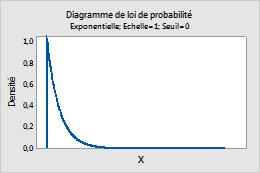
Par exemple, ce diagramme représente une loi exponentielle dont l'échelle est de 1 et le seuil de 0.

F

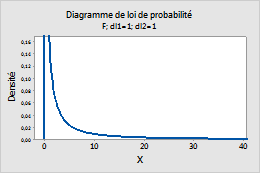
Dans Degrés de liberté du numérateur et Degrés de liberté du dénominateur, saisissez les degrés de liberté de numérateur et de dénominateur définissant la loi F. Pour plus d'informations, reportez-vous à la rubrique Loi F.

Par exemple, ce diagramme présente une loi F comportant 1 degré de liberté en numérateur et 1 degré de liberté en dénominateur.

Gamma

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi gamma.

  1. Dans la zone Paramètre de forme, saisissez la valeur qui représente la forme de la loi.
  2. Dans la zone Paramètre d'échelle, saisissez la valeur qui représente l'échelle de la loi.
  3. Dans la zone Paramètre de seuil, saisissez la borne inférieure de la loi.

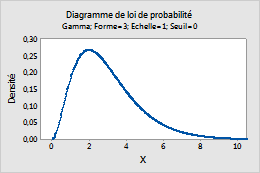
Par exemple, ce diagramme représente une loi gamma dont la forme est de 3, l'échelle de 1 et le seuil de 0.

Géométrique

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi géométrique.

  1. Dans la zone Probabilité d'événement, saisissez une valeur comprise entre 0 et 1 représentant la probabilité d'occurrence pour chaque essai. Une occurrence est appelée "événement".
  2. Pour indiquer la version de loi géométrique à utiliser, cliquez sur Options, puis sélectionnez l'une des options suivantes :
    • Modéliser le nombre total d'essais : modéliser le nombre total d'essais nécessaires pour produire un événement.
    • Modéliser le nombre de non-événements uniquement : modéliser le nombre de non-événements avant qu'un événement se produise.
    Conseil

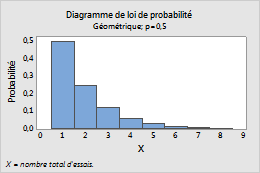
    Pour modifier les paramètres par défaut des sessions futures de Minitab, sélectionnez Fichier > Options > Commandes individuelles > Distributions.

Par exemple, ce diagramme représente une loi géométrique qui modélise le nombre total d'essais et dont la probabilité d'événement est de 0,5.

Hypergéométrique

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi hypergéométrique.

  1. Dans la zone Effectif de la population (N), saisissez le nombre total d'éléments dans la population (N). Si N est trop important pour être connu, la loi binomiale offre une approximation de la loi hypergéométrique.
  2. Dans la zone Nombre d'événements de la population (M), saisissez une valeur comprise entre 0 et N (effectif de la population) pour représenter le nombre d'événements compris dans la population.
  3. Dans la zone Effectif d'échantillon (n), saisissez le nombre d'éléments qui sont échantillonnés sans remise.

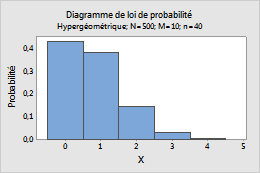
Par exemple, ce diagramme représente une loi hypergéométrique avec une population de 400, 10 événements et un effectif d'échantillon de 40.

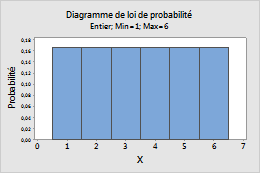
Entier

Suivez la procédure ci-dessous pour saisir les paramètres de la Distribution des entiers.

  1. Dans la zone Valeur minimale, saisissez le point situé à l'extrémité inférieure de la loi.
  2. Dans la zone Valeur maximale, saisissez le point situé à l'extrémité supérieure de la loi.

Par exemple, ce diagramme représente une loi de distribution des entiers avec une valeur minimale de 1 et une valeur maximale de 6.

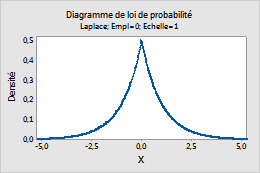
Laplace

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi de Laplace.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi de distribution.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi de distribution.

Par exemple, ce diagramme représente une loi de Laplace dont l'emplacement est de 0 et l'échelle de 1.

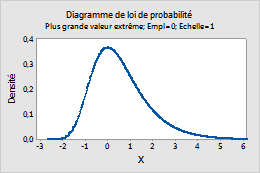
Plus grande valeur extrême

Suivez la procédure ci-dessous pour saisir les paramètres de la loi des plus grandes valeurs extrêmes. Pour plus d'informations, reportez-vous à la rubrique Lois de distribution des plus grandes et des plus petites valeurs extrêmes.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi de distribution.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi de distribution.

Par exemple, ce diagramme représente une loi des plus grandes valeurs extrêmes dont l'emplacement est de 0 et l'échelle de 1.

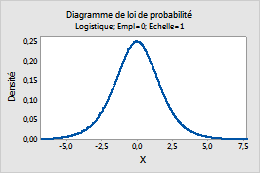
Logistique

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi de distribution logistique.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi de distribution.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi de distribution.

Par exemple, ce diagramme représente une loi logistique dont l'emplacement est de 0 et l'échelle de 1.

Log-logistique

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi log-logistique.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi logistique correspondante.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi logistique correspondante.
  3. Dans la zone Seuil, saisissez la borne inférieure de la loi.

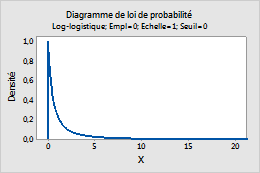
Par exemple, ce diagramme représente une loi log-logistique dont l'emplacement est de 0, l'échelle de 1 et le seuil de 0.

Log-normale

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi log-normale.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi normale correspondante.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi normale correspondante.
  3. Dans la zone Seuil, saisissez la borne inférieure de la loi.

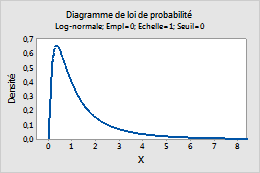
Par exemple, ce diagramme représente une loi log-normale dont l'emplacement est de 0, l'échelle de 1 et le seuil de 0.

Normale multivariée

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi normale multivariée.

  1. Dans Colonne des moyennes, saisissez la colonne contenant le vecteur de moyennes.
  2. Dans Matrice de variance/covariance, indiquez la matrice (par exemple, M1) contenant les variances et covariances des variables dans le même ordre que dans la colonne des moyennes.

Dans cet exemple, les données proviennent de trois variables corrélées, aléatoires et normales. Les moyennes sont en C1 et la matrice de variance-covariance est dans les colonnes C2-C4.

C1 C2 C3 C4
       
2,0 13,0321 2,6544 0,0899
100,1 2,6544 6,5883 1,4438
151,3 0,0899 1,4438 12,2219

Minitab doit d'abord lire la matrice de variance-covariance, puis la stocker.
  1. Sélectionnez Données > Copier > Colonnes dans matrice.
  2. Dans la zone Copier à partir des colonnes, saisissez C2-C4.
  3. Dans la zone Stocker les données copiées, sous Dans la feuille de travail en cours, dans la matrice :, saisissez M1.
  4. Cliquez sur OK.

Maintenant, vous pouvez générer des données aléatoires à partir de la loi normale multivariée.

  1. Sélectionnez Calc > Données aléatoires > Normale multivariée.
  2. Dans Nombre de lignes de données à générer, indiquez le nombre de lignes que vous souhaitez. Pour cet exemple, saisissez 18.
  3. Dans Stocker dans des colonnes, indiquez vos colonnes de stockage. Pour cet exemple, saisissez C6-C8.
  4. Dans Colonne des moyennes, indiquez la colonne contenant les moyennes. Pour cet exemple, saisissez C1.
  5. Dans Matrice de variance/covariance, indiquez la matrice. Pour cet exemple, saisissez M1.
  6. Cliquez sur OK.
Conseil

Pour obtenir le même échantillon que dans le tableau ci-dessous, définissez la base du générateur aléatoire avant de générer l'échantillon aléatoire. Sélectionnez Calc > Définir la base et saisissez 5.

C6 C7 C8
     
1,61033 99,192 148,814
0,45883 96,093 144,679
−0,46745 101,041 148,936
… … …

Binomiale négative

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi binomiale négative.

  1. Dans la zone Probabilité d'événement, saisissez une valeur comprise entre 0 et 1 représentant la probabilité d'occurrence pour chaque essai. Une occurrence est appelée "événement".
  2. Dans la zone Nombre d'événements nécessaires, saisissez un nombre entier positif qui représente le nombre de fois que l'événement doit se produire.
  3. Pour indiquer la version de loi binomiale négative à utiliser, cliquez sur Options, puis sélectionnez l'une des options suivantes :
    • Modéliser le nombre total d'essais : modéliser le nombre total d'essais nécessaires pour produire le nombre d'événements spécifié.
    • Modéliser le nombre de non-événements uniquement : modéliser le nombre de non-événements avant que le nombre d'événements spécifié se produise.
    Conseil

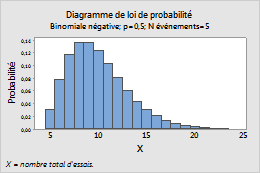
    Pour modifier les paramètres par défaut des sessions futures de Minitab, sélectionnez Fichier > Options > Commandes individuelles > Distributions.

Par exemple, ce diagramme représente une loi binomiale négative qui modélise le nombre total d'essais, et qui possède une probabilité d'événement de 0,5 et 5 événements.

Normale

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi normale.

  1. Dans la zone Moyenne, saisissez la valeur correspondant au centre de la loi.
  2. Dans la zone Ecart type, saisissez la valeur représentant la dispersion de la loi.

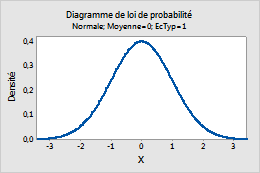
Par exemple, ce diagramme présente une loi normale dont la moyenne est de 0 et l'écart type de 1.

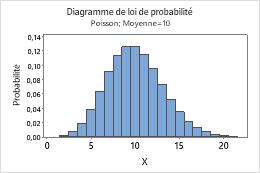
Poisson

Dans la zone Moyenne, saisissez le taux d'occurrence moyen. Pour plus d'informations, reportez-vous à la rubrique Loi de Poisson.

Par exemple, ce diagramme représente une loi de Poisson dont la moyenne est de 10.

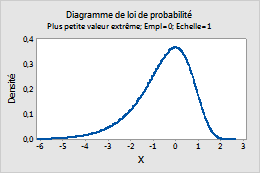
Plus petite valeur extrême

Suivez la procédure ci-dessous pour saisir les paramètres de la loi des plus petites valeurs extrêmes. Pour plus d'informations, reportez-vous à la rubrique Lois de distribution des plus grandes et des plus petites valeurs extrêmes.

  1. Dans la zone Emplacement, saisissez une valeur qui représente l'emplacement du pic de la loi de distribution.
  2. Dans la zone Echelle, saisissez une valeur qui représente la dispersion de la loi de distribution.

Par exemple, ce diagramme représente une loi des plus petites valeurs extrêmes dont l'emplacement est de 0 et l'échelle de 1.

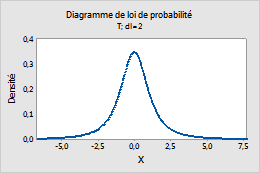
t

Dans la zone Degrés de liberté, saisissez les degrés de liberté définissant la loi t. Pour plus d'informations, reportez-vous à la rubrique Loi t.

Par exemple, ce diagramme présente une loi t comportant 2 degrés de liberté.

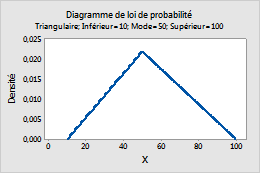
Triangulaire

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi triangulaire.

  1. Dans la zone Borne inférieure, saisissez la valeur minimale de la loi.
  2. Dans la zone Mode, saisissez la valeur correspondant au pic de la loi.
  3. Dans la zoneBorne supérieure, saisissez la valeur maximale de la loi.

Par exemple, ce diagramme représente une loi triangulaire dont la borne inférieure est de 10, le mode de 50 et la borne supérieure de 100.

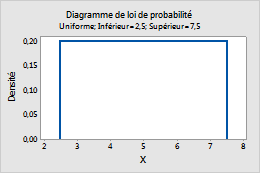
Uniforme

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi uniforme.

  1. Dans la zone Borne inférieure, saisissez la valeur minimale de la loi.
  2. Dans la zoneBorne supérieure, saisissez la valeur maximale de la loi.

Par exemple, ce diagramme représente une loi uniforme dont la borne inférieure est de 2,5 et la borne supérieure de 7,5.

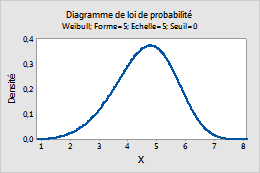
Weibull

Suivez la procédure ci-dessous pour saisir les paramètres de la Loi de Weibull.

  1. Dans la zone Paramètre de forme, saisissez la valeur qui représente la forme de la loi.
  2. Dans la zone Paramètre d'échelle, saisissez la valeur qui représente l'échelle de la loi.
  3. Dans la zone Paramètre de seuil, saisissez la borne inférieure de la loi.

Par exemple, ce diagramme présente une loi de Weibull dont l'emplacement est de 5, l'échelle de 5 et le seuil de 0.

Copyright © 2024 Minitab, LLC. All rights Reserved.