Sur ce thème
Moyenne
La moyenne est une mesure courante du centre d'un ensemble de valeurs numériques. Il s'agit de la somme de toutes les observations divisée par le nombre d'observations (présentes).
Formule
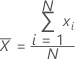
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
| N | nombre d'observations présentes |
Ecart type (EcTyp)
L'écart type de l'échantillon fournit une mesure de l'étendue de vos données. Il est égal à la racine carrée de la variance de l'échantillon.
Formule
 , l'écart type de l'échantillon est :
, l'écart type de l'échantillon est :
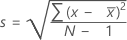
Notation
| Terme | Description |
|---|---|
| x i | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
Variance
La variance mesure le degré de dispersion des données autour de leur moyenne. Elle est égale à l'écart type au carré.
Formule
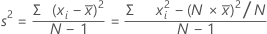
Notation
| Terme | Description |
|---|---|
| xi | ie observation |
 | moyenne des observations |
| N | nombre d'observations présentes |
Somme
Formule

Notation
| Terme | Description |
|---|---|
| xi | ie observation |
Minimum
Plus petite valeur de votre ensemble de données.
Médiane
La médiane de l'échantillon se trouve au milieu des données : au moins la moitié des observations lui est inférieure ou égale, et au moins la moitié lui est supérieure ou égale.
Supposez qu'une colonne contient N valeurs. Pour calculer la médiane, vous devez d'abord classer vos valeurs de données de la plus petite à la plus grande. Si N est impair, la médiane de l'échantillon est la valeur centrale. Si N est pair, la médiane de l'échantillon est la moyenne des deux valeurs centrales.
Par exemple, lorsque N = 5 et que vous avez les données x1, x2, x3, x4 et x5, la médiane est = x3.
Lorsque N = 6 et que vous avez classé les données x1, x2, x3, x4, x5 et x6 :
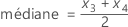
où x3 et x4 sont les troisième et quatrième observations.
Maximum
Plus grande valeur de votre ensemble de données.
Proportion de l'échantillon observé
Formule

Notation
| Terme | Description |
|---|---|
| x | nombre d'événements dans l'échantillon d'origine |
| N | nombre d'essais dans l'échantillon d'origine |
Moyenne de l'échantillon bootstrap
Formule
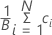
Remarque
Pour analyser une proportion, Minitab n'effectue pas de rééchantillonnages dans la colonne de données d'origine. Minitab recueille plutôt les rééchantillonnages par échantillonnage aléatoire à partir d'une loi binomiale. Le nombre d'essais et la probabilité d'événement de la distribution sont établis à partir de l'échantillon d'origine.
Notation
| Terme | Description |
|---|---|
| ci | Statistique choisie du ième rééchantillonnage |
| B | nombre de rééchantillonnages |
| N | nombre d'observations dans l'échantillon d'origine |
Ecart type de la distribution bootstrap
Formule

Notation
| Terme | Description |
|---|---|
 | moyenne de la statistique des rééchantillonnages choisie |
| B | nombre de rééchantillonnages |
| ci | statistique choisie du ième rééchantillonnage |
L'intervalle de confiance pour la statistique choisie
Formule
Trier la statistique des rééchantillonnages choisie par ordre croissant. x1 est le nombre le plus bas, xB le nombre le plus élevé.
Borne inférieure : x1 où = 
Borne supérieure : xu où = 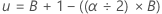
Pour analyser une proportion, Minitab ne prélève pas de rééchantillonnages sur la colonne de données d'origine. Minitab recueille plutôt les rééchantillonnages par prélèvement aléatoire à partir d'une loi binomiale. Le nombre d'essais et la probabilité d'événement de la distribution sont établis à partir de l'échantillon d'origine.
Remarque
Pour un cas unilatéral (une borne inférieure ou supérieure uniquement), utilisez α au lieu de α/2.
Lorsque 1 ou u ne sont pas des nombres entiers, Minitab effectue une interpolation linéaire entre les deux nombres de chaque côté de 1 ou de u.
Xy + z(Xy+1 - Xy)
Par exemple, si 1 = 5,25, la borne inférieure est égale à x5 + 0,25(x6 - x5).
Minitab n'affiche pas l'intervalle de confiance lorsque  ou
ou 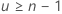 .
.
Notation
| Terme | Description |
|---|---|
| α | 1 – niveau de confiance/100 |
| B | nombre de rééchantillonnages |
| Xy | yème ligne des données, lorsque celles-ci sont classées de la plus petite à la plus grande |
| y | valeur tronquée de l ou u |
| z | l-y ou u - y |
