Sur ce thème
Histogramme
Un histogramme divise les valeurs des échantillons en plusieurs intervalles et représente l'effectif des valeurs contenues dans chaque intervalle par une barre.
Interprétation
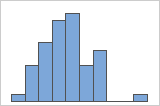
50 rééchantillonnages
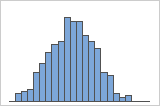
1 000 rééchantillonnages
La loi de distribution est généralement plus facile à déterminer avec davantage de rééchantillonnages. Par exemple, dans ces données, la loi de distribution est ambiguë pour 50 rééchantillonnages. Avec 1 000 rééchantillonnages, la forme est approximativement normale.
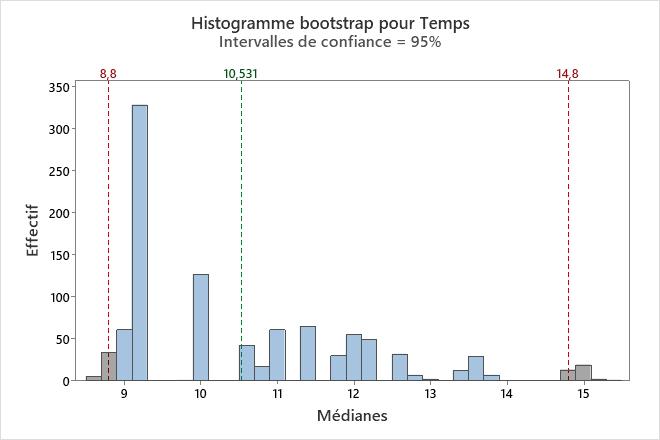
Sur cet histogramme, la distribution bootstrap semble anormale. L'échantillon d'origine ne contient que 16 points de données. Pour obtenir un intervalle de confiance fiable, vous devez collecter un échantillon plus important et effectuer à nouveau l'analyse.
Diagramme des valeurs individuelles
Un diagramme des valeurs individuelles présente les valeurs individuelles contenues dans l'échantillon. Chaque cercle représente une observation. Un diagramme des valeurs individuelles est particulièrement utile lorsque vous disposez de relativement peu d'observations et que vous avez besoin d'évaluer l'effet de chacune d'entre elles.
Remarque
Minitab présente un diagramme des valeurs individuelles seulement lorsque vous effectuez un rééchantillonnage. Minitab présente les données d'origine et celles du rééchantillonnage.
Interprétation
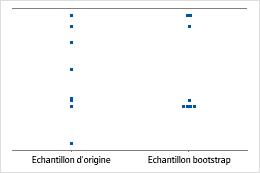
effectif de l'échantillon égal à 8
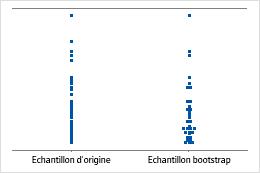
effectif de l'échantillon égal à 50
Carte barre
La carte barre illustre la proportion d'occurrences dans chaque catégorie.
Remarque
Minitab affiche une carte barre lorsque vous effectuez un seul rééchantillonnage. Minitab affiche à la fois les données d'origine et celles du rééchantillonnage.
Interprétation
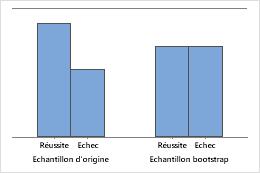
Effectif de l'échantillon égal à 8
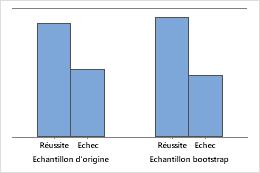
Effectif de l'échantillon égal à 50
Nombre de rééchantillonnages
Le nombre de rééchantillonnages est le nombre de fois que Minitab prélève un échantillon aléatoire avec remise dans votre ensemble de données d'origine. Généralement, un grand nombre de rééchantillonnages donne de meilleurs résultats. L'effectif d'échantillon pour chaque rééchantillonnage est égal à l'effectif d'échantillon de l'ensemble de données d'origine. Le nombre de rééchantillonnages est égal au nombre d'observations dans l'histogramme.
Moyenne
La moyenne est la somme des statistiques de l'échantillon bootstrap choisies divisée par le nombre de rééchantillonnages.
Interprétation
Minitab affiche deux valeurs de différence de la statistique choisie : la valeur de l'échantillon observé et celle de la distribution bootstrap (moyenne). Ces deux valeurs sont une estimation du paramètre de population et sont généralement similaires. En cas de différence importante entre ces deux valeurs, augmentez l'effectif de vos échantillons d'origine.
La moyenne étant calculée à partir de données d'échantillon et non de l'ensemble de la population, il est peu probable qu'elle soit égale au paramètre de population. Pour mieux estimer la moyenne de la population, utilisez l'intervalle de confiance.
EcTyp (échantillon bootstrap)
L'écart type des échantillons bootstrap (également appelé erreur type bootstrap) est une estimation de l'écart type de la loi d'échantillonnage de la statistique choisie.
Interprétation
Utilisez l'écart type pour déterminer la dispersion des statistiques de l'échantillon bootstrap choisies par rapport à la moyenne globale. Une valeur d'écart type élevée indique une plus grande dispersion.
Utilisez l'écart type des échantillons bootstrap pour déterminer avec quelle précision la statistique bootstrap évalue le paramètre de la population. Lorsque la valeur est moins élevée, l'estimation du paramètre de la population est plus précise. En revanche, plus l'effectif d'échantillon est élevé, plus l'erreur type bootstrap sera faible et plus l'estimation du paramètre de population sera précise.
Bornes et intervalle de confiance (IC)
Les intervalles de confiance pour l'écart type sont fondés sur la distribution d'échantillonnage d'une statistique. Si une statistique ne dispose pas d'un biais sous forme d'estimateur d'un paramètre, sa distribution d'échantillonnage est centrée sur la valeur réelle du paramètre. Une distribution bootstrap se rapproche de la distribution d'échantillonnage de la statistique. 95 % des valeurs du milieu de la distribution bootstrap fournissent donc un intervalle de confiance à 95 % pour le paramètre. L'intervalle de confiance vous aide à évaluer la signification pratique de votre estimation pour le paramètre de population. Utilisez vos connaissances spécialisées pour déterminer si l'intervalle de confiance comporte des valeurs ayant une signification pratique pour votre situation.
Remarque
Minitab ne calcule pas l'intervalle de confiance lorsque le nombre de rééchantillonnages est trop petit pour obtenir un intervalle de confiance précis.
Echantillon observé
| Variable | N | Moyenne | EcTyp | Variance | Somme | Minimum | Médiane | Maximum |
|---|---|---|---|---|---|---|---|---|
| Temps | 16 | 11,331 | 3,115 | 9,702 | 181,300 | 7,700 | 10,050 | 16,000 |
Echantillons bootstrap pour la moyenne
| Nombre de rééchantillonnages | Moyenne | EcTyp | IC à 95% pour μ |
|---|---|---|---|
| 1000 | 11,3095 | 0,7625 | (9,8562; 12,8562) |
Dans ces résultats, l'estimation de la moyenne de la population est d'environ 11,3. Vous pouvez être sûr à 95 % que la moyenne de la population se trouve environ entre 9,9 et 12,9.
