Le diagramme de probabilité crée, à partir de l'échantillon, une fonction de répartition cumulée (CDF) estimée en traçant la valeur de chaque observation (y compris les valeurs répétées) par rapport à sa probabilité cumulée estimée.
Minitab calcule la probabilité cumulée estimée à l'aide de l'une des formules suivantes, en fonction des valeurs sélectionnées dans (la valeur par défaut est le rang médian). Pour chaque formule, n représente le nombre d'observations et i le rang de chaque observation, avec i = 1 pour la valeur la plus basse et i = n pour la valeur la plus élevée.
- Rang de médiane (Benard)
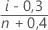
- Rang de moyenne (Herd-Johnson)

- Kaplan-Meier modifié (Hazen)
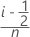
- Kaplan-Meier

Remarque
La méthode Kaplan-Meier donne p = 1 pour l'observation la plus élevée. La valeur obtenue ne pouvant pas être utilisée dans le diagramme, Minitab calcule donc le plus grand p comme 90 % de la distance entre le précédent p et 1.
La droite d'ajustement représente la fonction de répartition de la distribution théorique sélectionnée, avec les paramètres indiqués (estimés ou historiques). Si vous ne fournissez pas de paramètres historiques, Minitab les évalue à l'aide de la méthode d'estimation par les moindres carrés (loi normale ou log-normale) ou de l'estimation par le maximum de vraisemblance (autres lois).
Les valeurs y (et, dans certains cas, les valeurs x) sont transformées de manière à ce que la ligne d'ajustement soit une droite. Toutefois, les étiquettes de repères demeurent cohérentes avec les valeurs non transformées. Par conséquent, dans la mesure où la loi sélectionnée s'ajuste aux données, les points relevés forment une ligne droite.
Le tableau suivant indique les transformations utilisées pour chaque loi.
| Loi de distribution | Coordonnée X | Coordonnée Y |
|---|---|---|
| Normale | données | |
| Log-normale | ln(données) | |
| Log-normale à 3 paramètres | ln(données - seuil) | |
| Gamma | ln(données) | G-1(p), k |
| Gamma à 3 paramètres | ln(données - seuil) | G-1(p), k |
| Exponentielle | ln(données) | ln(-ln(1 - p)) |
| Exponentielle à 2 paramètres | ln(données - seuil) | ln(-ln(1 - p)) |
| Plus petites valeurs extrêmes | données | ln(-ln(1 - p)) |
| Weibull | ln(données) | ln(-ln(1 - p)) |
| Weibull à 3 paramètres | ln(données - seuil) | ln(-ln(1 - p)) |
| Plus grande valeur extrême | données | -ln(-ln(p)) |
| Logistique | données |
 |
| Log-logistique | ln(données) |
 |
| Log-logistique à 3 paramètres | ln(données - seuil) |
 |
Important
Si vous tracez des données non ajustées pour le seuil, l'ajustement de la distribution n'est pas représenté par une ligne droite.
Notation
| Terme | Description |
|---|---|
| données | valeur de données pour l'observation |
| In(x) | logarithme népérien de x |
| valeur renvoyée pour p par la fonction de répartition inverse pour la loi normale standard. | |
| G-1(p),k | valeur renvoyée pour p par la fonction de répartition inverse pour une loi Gamma de forme k et d'échelle 1. Minitab utilise le paramètre de forme estimé sauf si vous entrez une valeur historique. |
