Sur ce thème
Etape 1 : Déterminer si les données ne respectent pas la loi de distribution
- Valeur de p ≤ α : les données ne suivent pas la loi (Rejeter H0)
- Si la valeur de p est inférieure ou égale au seuil de signification, vous pouvez rejeter l'hypothèse nulle et en conclure que vos données ne suivent pas la loi.
- Valeur de p > α : impossible de conclure que les données ne suivent pas la loi (Impossible de rejeter H0)
- Si la valeur de p est supérieure au seuil de signification, vous ne pouvez pas rejeter l'hypothèse nulle, car vous n'êtes pas en mesure de conclure que les données ne suivent pas la loi. Néanmoins, vous ne pouvez pas en conclure que les données suivent la loi.
Pour obtenir des informations sur la spécification de différents paramètres et lois de distribution pour le test, reportez-vous à la rubrique Lignes de distribution ajustées.
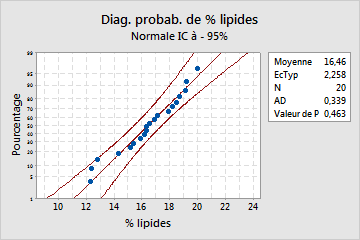
Résultats principaux : valeur de p
Dans ces résultats, l'hypothèse nulle indique que les données suivent la loi de distribution normale. La valeur de p étant de 0,463, ce qui est supérieur au seuil de signification de 0,05, vous ne pouvez pas rejeter l'hypothèse nulle. Vous ne pouvez pas en conclure que les données ne suivent pas la loi de distribution normale.
Mise en garde
L'effectif de l'échantillon influe sur la puissance du test. Des échantillons extrêmement petits ne permettent pas forcément de détecter des écarts significatifs par rapport à la loi. Les échantillons très grands risquent de détecter trop de petits écarts sans conséquences par rapport à la loi. Utilisez donc les résultats visuels du diagramme de probabilité, ainsi que les valeurs de p, pour évaluer l'ajustement d'une loi, comme montré à l'étape 2.
Etape 2 : Visualiser l'ajustement de la loi de distribution
Examinez le diagramme de probabilité et regardez si les points de données suivent la droite de distribution ajustée de façon étroite ou lâche. Si les lois théoriques spécifiées sont bien ajustées, les points sont répartis sur une ligne droite. Par exemple, les points sur la droite de Henry suivent la ligne de près. La loi de distribution normale semble bien correspondre aux données.
Remarque
La droite de distribution ajustée est une ligne droite centrale sur le diagramme. Les lignes pleines placées aux extrémités du diagramme sont des intervalles de confiance pour les percentiles individuels, pas pour la loi entière, et ne doivent pas être utilisés pour évaluer l'ajustement de la loi.
Pour plus d'informations sur l'évaluation visuelle des valeurs du diagramme de probabilité, reportez-vous à la rubrique Droites de Henry et "test du crayon gras".
Etape 3 : Afficher les percentiles estimés de la population
Dans Minitab, maintenez le curseur sur la droite de distribution ajustée pour afficher le tableau des percentiles et des valeurs.
Par exemple, le diagramme de probabilité suivant montre le pouls des sujets de l'étude qui marchent sur un tapis roulant. Pour une loi normale avec une moyenne et un écart type identiques aux données, nous nous attendrions à ce que 5 % de la population ait un pouls maximal de 54,76.
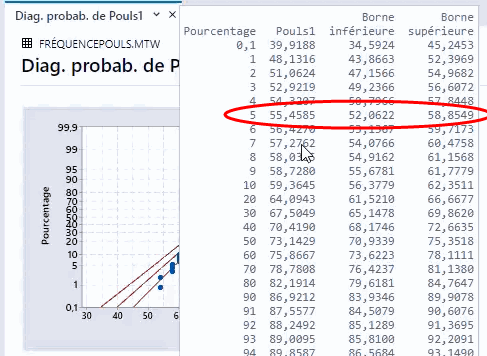
Remarque
Les percentiles estimés de la population sont seulement exacts si les données respectent minutieusement la loi.
