Sur ce thème
- Fonction de répartition
- Probabilité cumulée inverse
- Fonction de densité de probabilité
- Loi bêta
- Loi binomiale
- Loi de Cauchy
- Loi du Khi deux
- Loi discrète
- Loi exponentielle
- Loi F
- Loi gamma
- Distribution géométrique
- Loi hypergéométrique
- Distribution des entiers
- Loi de Laplace
- Loi avec valeur extrême la plus grande
- Loi de distribution logistique
- Loi log-logistique
- Loi log-normale
- Loi binomiale négative
- Loi normale
- Loi de Poisson
- Loi des plus petites valeurs extrêmes
- Loi t
- Loi triangulaire
- Loi uniforme
- Loi de Weibull
Fonction de répartition
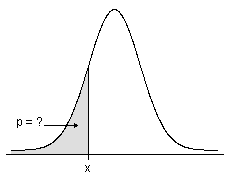
- Pour les lois continues, la CDF permet d'obtenir l'aire située sous la fonction de densité de probabilité jusqu'à la valeur de x que vous indiquez.
- Pour les lois discrètes, la CDF permet d'obtenir la probabilité cumulée correspondant aux valeurs x que vous indiquez.
Probabilité cumulée inverse
Pour un nombre p compris dans l'intervalle fermé [0,1], la fonction de répartition inverse (CDF inverse) d'une variable aléatoire X détermine, lorsque c'est possible, une valeur de x pour laquelle la probabilité que X ≤ x est supérieure ou égale à p.
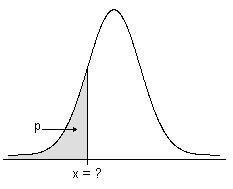
- CDF inverse pour les lois continues
-
La CDF inverse fournit la valeur associée à une aire située sous la fonction de densité de probabilité. Il s'agit de l'inverse de la fonction de répartiton (CDF), qui fournit quant à elle l'aire associée à une valeur.
Pour toutes les lois continues, la CDF inverse existe et est unique si 0 < p < 1.
- Lorsque la fonction de densité de probabilité (PDF) est positive pour l'ensemble de la ligne de nombres réels (par exemple, la PDF normale), la CDF inverse n'est pas définie soit pour p = 0, soit pour p = 1.
- Lorsque la PDF est positive pour toutes les valeurs qui sont supérieures à une valeur donnée (par exemple, la PDF du Khi deux), la CDF inverse est définie pour p = 0, mais pas pour p = 1.
- Lorsque la PDF est uniquement positive sur un intervalle (par exemple, la PDF de la loi uniforme), la CDF inverse est définie pour p = 0 et pour p = 1.
- Dans les cas où la CDF inverse n'est pas définie, Minitab renvoie une valeur manquante (*) pour le résultat.
- CDF inverse pour les lois discrètes
- La CDF inverse est plus complexe pour les lois discrètes que pour les lois continues. Lorsque vous calculez la CDF correspondant à une loi binomiale avec, par exemple, n = 5 et p = 0,4, il n'existe aucune valeur x pour laquelle la CDF est égale à 0,5. Pour x = 1, la CDF est de 0,3370. Pour x = 2, la CDF passe à 0,6826.
Fonction de densité de probabilité
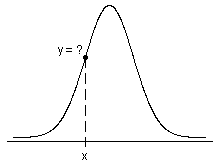
- Pour les lois continues, la probabilité que des valeurs de X soient comprises dans un intervalle (a, b) correspond précisément à l'aire se trouvant sous sa PDF dans l'intervalle (a, b).
- Pour les lois discrètes, la probabilité que des valeurs de X soient comprises dans un intervalle (a, b) correspond précisément à la somme de la PDF (aussi appelée fonction de masse de probabilité) des valeurs discrètes de X possibles dans (a, b).
Loi bêta
La loi bêta est souvent utilisée pour représenter les procédés ayant des limites inférieure et supérieure naturelles.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :

Notation
| Terme | Description |
|---|---|
| α | paramètre de forme 1 |
| β | paramètre de forme 2 |
| Γ | Fonction gamma |
| a | limite inférieure |
| b | limite supérieure |
Lorsque a = 0 et b = 1,
la PDF est calculée comme suit :
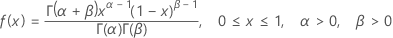


Loi binomiale
La loi binomiale permet de représenter le nombre d'événements qui se produisent au cours de n essais indépendants. Les valeurs possibles sont des nombres entiers compris entre zéro et n.
Formule
moyenne = np
variance = np(1 – p)
La fonction de masse de probabilité (PMF) est exprimée comme suit :
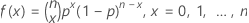
Où  est égal à
est égal à  .
.
En règle générale, vous pouvez calculer k! comme suit : 
Notation
| Terme | Description |
|---|---|
| n | nombre d'essais |
| x | nombre d'événements |
| p | probabilité d'événement |
Loi de Cauchy
La loi de Cauchy est symétrique autour de zéro, mais ses extrémités avoisinent moins rapidement zéro que celles de la loi normale.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
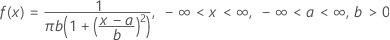
Notation
| Terme | Description |
|---|---|
| a | paramètre d'emplacement |
| b | paramètre d'échelle |
| π | Pi (~3,142) |
Remarque
Si vous ne spécifiez pas de valeur, Minitab utilise a = 0 et b = 1.
Loi du Khi deux
Si X présente une loi normale standard, X2 présente une loi du Khi deux avec un degré de liberté, ce qui en fait une loi d'échantillonnage couramment utilisée.
La somme de n variables X2 indépendantes (où X suit une loi normale standard) obéit à une loi du Khi deux à n degrés de liberté. La forme de la loi du Khi deux dépend du nombre de degrés de liberté.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
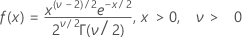
moyenne = v
variance = 2v
Notation
| Terme | Description |
|---|---|
| ν | degrés de liberté |
| Γ | fonction gamma |
| e | base du logarithme népérien |
Loi discrète
Une loi de probabilité discrète est une loi que vous définissez vous-même. Supposons que vous êtes intéressé par une distribution constituée de trois valeurs −1, 0, 1, avec des probabilités respectives de 0,2, 0,5 et 0,3. Si vous saisissez les valeurs dans les colonnes d'une feuille de travail, vous pouvez les utiliser pour générer des données aléatoires ou pour calculer des probabilités.
| Valeur | Prob |
|---|---|
| −1 | 0,2 |
| 0 | 0,5 |
| 1 | 0,3 |
Loi exponentielle
La loi exponentielle peut être utilisée pour modéliser le temps écoulé entre des défaillances, par exemple quand des unités ont un taux de défaillance constant et instantané (fonction de risque). La loi exponentielle est un cas particulier de la loi de Weibull et de la loi gamma.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
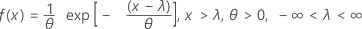
La fonction de répartition (CDF) est calculée comme suit :

moyenne = θ + λ
variance = θ2
Notation
| Terme | Description |
|---|---|
| θ | paramètre d'échelle |
| λ | paramètre de seuil |
| exp | base du logarithme népérien |
Remarque
Certaines références utilisent 1/θ en tant que paramètre.
Loi F
La loi F est aussi connue sous le nom de loi variance-rapport et présente deux types de degrés de liberté : les degrés de liberté de numérateur et de dénominateur. Il s'agit de la loi de distribution du rapport de deux variables aléatoires indépendantes suivant des lois du Khi deux, chacune divisée par ses degrés de liberté.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
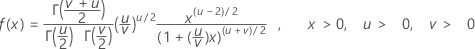
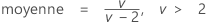
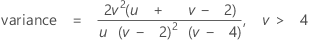
Notation
| Terme | Description |
|---|---|
| Γ | Fonction gamma |
| u | degrés de liberté du numérateur |
| v | degrés de liberté du dénominateur |
Loi gamma
La loi gamma est souvent utilisée pour modéliser des données asymétriques dans le sens positif.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :

moyenne = ab + θ
variance = ab2
Notation
| Terme | Description |
|---|---|
| a | paramètre de forme (lorsque a = 1, la PDF de gamma est identique à la PDF exponentielle) |
| b | paramètre d'échelle |
| θ | paramètre de seuil |
| Γ | fonction gamma |
| e | base du logarithme népérien |
Remarque
Certaines références utilisent 1/b en tant que paramètre.
Distribution géométrique
La loi géométrique négative discrète s'applique à une suite d'expériences de Bernoulli indépendantes portant sur un événement d'intérêt ayant une probabilité p.
Formule
Si la variable aléatoire X est le nombre total d'essais nécessaires pour produire un événement avec une probabilité p, la fonction de masse de probabilité (PMF) de X est obtenue de la façon suivante :

et X présente les propriétés suivantes :


Si la variable aléatoire Y correspond au nombre de non-événements qui se produisent avant que le premier événement (avec la probabilité p) soit observé, la fonction de masse de probabilité (PMF) de Y est obtenue de la façon suivante :

et Y présente les propriétés suivantes :


Notation
| Terme | Description |
|---|---|
| X | nombre d'essais nécessaires pour produire un événement, Y + 1 |
| Y | nombre de non-événements qui se produisent avant le premier événement. |
| p | probabilité qu'un événement se produise pour chaque essai |
Loi hypergéométrique
La loi hypergéométrique est utilisée pour les échantillons prélevés auprès de populations restreintes, sans remise. Par exemple, supposons qu'un lot de N téléviseurs comporte N1 postes fonctionnels (succès) et N2 postes défectueux (échec). Si vous prélevez un échantillon aléatoire de n téléviseurs sur N sans remise, vous pouvez obtenir la probabilité pour qu'exactement x des n téléviseurs soient fonctionnels.
Formule
La fonction de masse de probabilité (PMF) est exprimée comme suit :
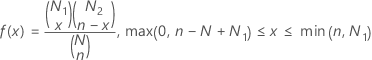


Notation
| Terme | Description |
|---|---|
| N | N1 + N2 = effectif de la population |
| N1 | nombre d'événements dans la population |
| N2 | nombre de non-événements dans la population |
| n | effectif d'échantillon |
| x | nombre d'événements dans l'échantillon |
Distribution des entiers
La loi de distribution des entiers est une loi uniforme discrète portant sur un ensemble d'entiers. Chaque entier a la même probabilité d'occurrence.
Loi de Laplace
La loi de Laplace est utilisée lorsque la loi est plus pointue qu'une loi normale.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
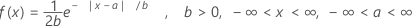
moyenne = a
variance = 2b2
Notation
| Terme | Description |
|---|---|
| a | paramètre d'emplacement |
| b | paramètre d'échelle |
| e | base du logarithme népérien |
Loi avec valeur extrême la plus grande
Utilisez la loi des plus grandes valeurs extrêmes pour modéliser la valeur la plus élevée d'une loi. Si vous disposez d'une suite de lois exponentielles et que X(n) est le maximum de la première valeur de n, la loi de distribution de X(n) – ln(n) converge avec la loi des plus grandes valeurs. De ce fait, pour des valeurs de n élevées, la loi des plus grandes valeurs extrêmes constitue une bonne approximation de la loi de distribution de X(n) – ln(n).
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :

La fonction de répartition (CDF) est calculée comme suit :

moyenne = μ + γσ
variance = π 2 σ 2 / 6
Notation
| Terme | Description |
|---|---|
| σ | paramètre d'échelle |
| μ | paramètre d'emplacement |
| γ | constante d'Euler (~0,57722) |
Loi de distribution logistique
Loi de distribution symétrique semblable à la loi normale, mais présentant des extrémités plus lourdes.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
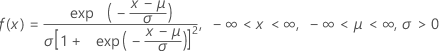
La fonction de répartition (CDF) est calculée comme suit :
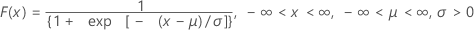
moyenne = μ
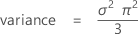
Notation
| Terme | Description |
|---|---|
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
Loi log-logistique
Une variable x suit une loi log-normale avec un seuil λ si Y = log (x – λ) suit une loi logistique.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
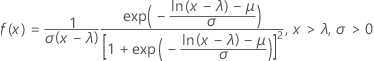
La fonction de répartition (CDF) est calculée comme suit :

quand σ < 1 :

quand σ < 1/2 :
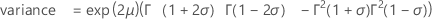
Notation
| Terme | Description |
|---|---|
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| λ | paramètre de seuil |
| Γ | fonction gamma |
| exp | base du logarithme népérien |
Loi log-normale
Une variable x suit une loi log-normale si log(x – λ) suit une loi normale.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :

La fonction de répartition (CDF) est calculée comme suit :



Notation
| Terme | Description |
|---|---|
| μ | paramètre d'emplacement |
| σ | paramètre d'échelle |
| λ | paramètre de seuil |
| π | Pi (~3,142) |
Loi binomiale négative
La loi binomiale négative discrète s'applique à une série d'expériences de Bernoulli indépendantes portant sur un événement d'intérêt ayant une probabilité p.
Formule
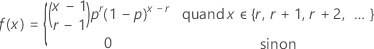


Si la variable aléatoire Y correspond au nombre de non-événements qui se produisent avant que vous observiez les r événements, qui ont chacun une probabilité p, la fonction de masse de probabilité (PMF) de Y est obtenue de la façon suivante :
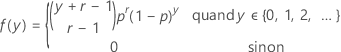
et Y présente les propriétés suivantes :


Remarque
Cette loi binomiale négative est également connue sous le nom de loi de Pascal.
Notation
| Terme | Description |
|---|---|
| X | Y + r |
| r | nombre d'événements |
| p | probabilité d'un événement |
Loi normale
La loi normale (aussi appelée loi de Gauss) est la loi statistique la plus utilisée en raison des nombreux procédés physiques, biologiques et sociaux qu'elle permet de modéliser.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
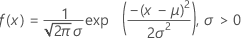
La fonction de répartition (CDF) est calculée comme suit :
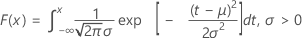
moyenne = μ
variance = σ 2
écart type = σ
Notation
| Terme | Description |
|---|---|
| exp | base du logarithme népérien |
| π | Pi (~3,142) |
Loi de Poisson
La loi de Poisson est une loi de probabilité discrète qui modélise un nombre d'événements à partir d'un taux d'occurrence constant. La loi de Poisson peut être utilisée comme approximation de la loi binomiale lorsque le nombre d'essais indépendants est élevé et que la probabilité de réussite est faible.
Formule
La fonction de masse de probabilité (PMF) est exprimée comme suit :
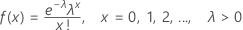
moyenne = λ
variance = λ
Notation
| Terme | Description |
|---|---|
| e | base du logarithme népérien |
Loi des plus petites valeurs extrêmes
Utilisez la loi des plus petites valeurs extrêmes pour modéliser la valeur la plus petite d'une loi. Si Y suit une loi de Weibull, alors Log(Y) suit une loi des plus petites valeurs extrêmes.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
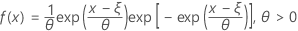
La fonction de répartition (CDF) est calculée comme suit :

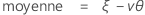

Notation
| Terme | Description |
|---|---|
| ξ | paramètre d'emplacement |
| θ | paramètre d'échelle |
| e | base du logarithme népérien |
| v | constante d'Euler (~0,57722) |
Loi t
- Créer des intervalles de confiance de la moyenne de population à partir d'une loi normale lorsque la variance est inconnue.
- Déterminer si deux moyennes d'échantillon provenant de populations normales avec des variances inconnues mais égales présentent une différence importante.
- Tester la signification des coefficients de régression.
Formule
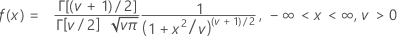
moyenne = 0, où ν > 0

Notation
| Terme | Description |
|---|---|
| Γ | Fonction gamma |
| v | degrés de liberté |
| π | Pi (~3,142) |
Loi triangulaire
La PDF de la loi triangulaire présente une forme triangulaire.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
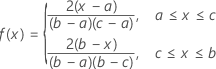

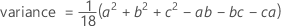
Notation
| Terme | Description |
|---|---|
| a | borne inférieure |
| b | borne supérieure |
| c | mode (emplacement du pic de la PDF) |
Loi uniforme
La loi uniforme caractérise les données d'un intervalle de manière uniforme, avec a comme plus petite valeur et b comme plus grande valeur.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :



Notation
| Terme | Description |
|---|---|
| a | borne inférieure |
| b | borne supérieure |
Loi de Weibull
La loi de Weibull permet de modéliser les temps de défaillance de produits.
Formule
La fonction de densité de probabilité (PDF) est calculée comme suit :
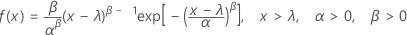
La fonction de répartition (CDF) est calculée comme suit :

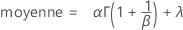
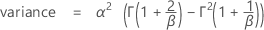
Notation
| Terme | Description |
|---|---|
| α | paramètre d'échelle |
| β | paramètre de forme, lorsque β = 1, la PDF de Weibull est identique à la PDF exponentielle |
| λ | paramètre de seuil |
| Γ | fonction gamma |
| exp | base du logarithme népérien |
Remarque
Certaines références utilisent 1/α en tant que paramètre.
