Sur ce thème
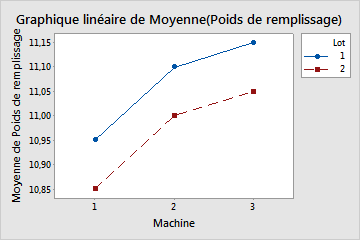
Etape 1 : Rechercher l'existence d'interactions
Si les lignes du diagramme ne sont pas parallèles, il existe peut-être une interaction. Une interaction indique que les moyennes des données Y aux niveaux de la première variable X sont différentes à chaque niveau de la seconde variable X. Moins les lignes sont parallèles, plus l'interaction est forte.
Remarque
Même si vous pouvez utiliser le graphique linéaire pour afficher les effets et les interactions, vous devez réaliser le test statistique approprié afin d'évaluer la signification statistique des effets ou des interactions que vous observez. Si les effets d'interaction sont significatifs, vous ne pouvez pas interpréter les effets principaux sans en tenir compte.
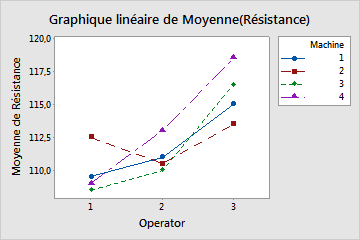
Etape 2 : Rechercher l'existence d'effets
Les lignes inclinées suggèrent la potentielle existence d'un effet en raison du facteur X. Les différences entre les lignes indiquent la potentielle existence d'un effet en raison du facteur de légende. Evaluez l'existence d'effets (ou l'absence d'effets) en lien avec les objectifs de votre étude.
- Objectif pour Y
- Recherchez les niveaux de variables X qui minimisent Y, maximisent Y ou se rapprochent d'une valeur cible Y.
- Robustesse de Y aux changements dans X
- Recherchez les niveaux d'une variable X qui rendent Y résistant aux changements dans l'autre variable X. Par exemple, déterminez si la moyenne de Y est presque la même pour tous les paramètres de la variable X sur l'axe S du graphique, ou pour tous les paramètres de la variable X dans la légende.