Etape 1 : Evaluer les caractéristiques clés
Examinez le centrage de la loi de distribution. Evaluez l'incidence de l'effectif de l'échantillon sur l'apparence du graphique des intervalles.
Centré
- Intervalle de confiance
- L'intervalle de confiance est une étendue de valeurs qui contient probablement la moyenne de la population.
- Moyenne de l'échantillon
- La moyenne de l'échantillon est représentée par un symbole.
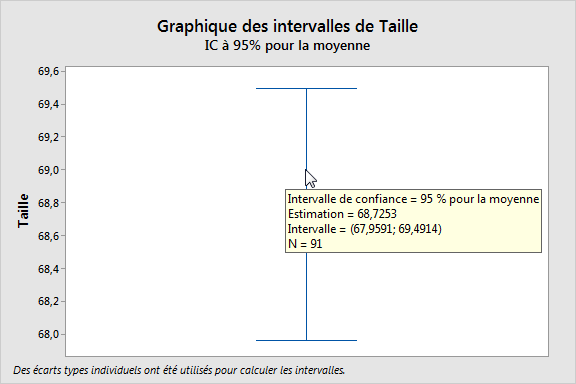
Etudiez les intervalles de confiance qui sont surprenants ou inattendus. Par exemple, si un intervalle de confiance pour la moyenne d'un échantillon de temps d'attente des clients est considérablement différent des intervalles de confiance d'échantillons précédents, vous devez essayer de déterminer la cause de cette différence.
Effectif d'échantillon (n)
L'effectif de l'échantillon peut avoir une incidence sur l'apparence du graphique.
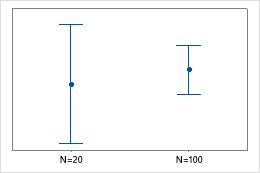
En général, plus l'effectif de l'échantillon est important, plus l'intervalle de confiance est réduit et précis. Si l'intervalle de confiance est trop important, essayez de collecter un échantillon plus important. Des différences importantes dans les effectifs d'échantillons entre des groupes (ou des variables Y multiples) peuvent avoir une incidence sur les largeurs des intervalles et générer des résultats trompeurs. Si les effectifs d'échantillons des groupes (ou des variables Y multiples) sont presque les mêmes, vous pouvez être plus certain que les différences des largeurs des intervalles sont essentiellement dues aux différences de variation.
Étape 2 : Évaluer et comparer des groupes
Si votre graphique des intervalles comporte des groupes, évaluez et comparez le centrage et la dispersion des groupes.
Centres
Déterminez si des intervalles de confiance se chevauchent. Si les intervalles de deux moyennes ne se chevauchent pas, les moyennes de population peuvent être statistiquement significatives.
Par exemple, dans le premier graphique des intervalles, le premier et le deuxième intervalles se chevauchent, mais ils ne chevauchent pas le troisième. Par conséquent, la moyenne du troisième groupe pourrait être statistiquement différente de la moyenne des deux autres groupes. Dans le deuxième graphique des intervalles, les intervalles ne se chevauchent pas. Ainsi, les différences entre les moyennes pourraient être statistiquement significatives.
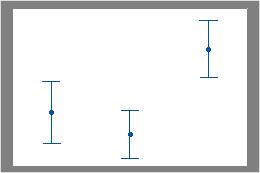
Certains intervalles se chevauchent
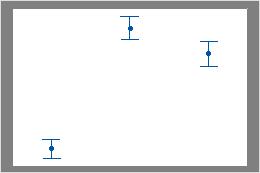
Aucun intervalle ne se chevauche
- Utilisez un test t à 2 échantillons si vous n'avez que deux groupes.
- Utilisez une ANOVA à un facteur contrôlé si vous n'avez que trois groupes ou plus.
Dispersions
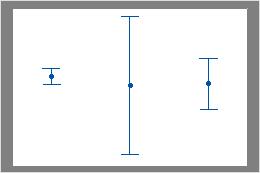
Recherchez les différences entre les dispersions des groupes.
Les intervalles de ce graphique ont des centres similaires mais des dispersions différentes.
Conseil
Pour savoir si une différence dans une largeur d'intervalle est due à une différence dans la variation de l'effectif ou dans l'effectif de l'échantillon, double-cliquez sur un intervalle. Dans l'onglet Options, cliquez sur Regrouper les erreurs dans les groupes. Vous recréez ainsi les intervalles avec écart type regroupé plutôt qu'avec les écarts types individuels. Toute différence de largeur que vous observez à présent est strictement due à la différence des effectifs d'échantillons.
- Utilisez un test à 2 variances si vous n'avez que deux groupes.
- Utilisez un test de l'égalité des variances si vous avez trois groupes ou plus.
