Loi exponentielle
Utilisez la loi exponentielle pour modéliser le temps écoulé entre des événements dans un procédé de Poisson continu. Nous considérons que les événements indépendants surviennent à une fréquence constante.
Cette loi a une multitude d'applications, dont les analyses de fiabilité des produits et des systèmes, la théorie des files d'attente et les chaînes de Markov.
- Le temps avant défaillance de composants électroniques
- L'intervalle de temps entre les arrivées des clients à un guichet
- Le temps avant que les clients de la file d'attente ne soient servis
- Le temps avant un défaut de paiement (modélisation du risque de crédit)
- Le temps de demie-vie d'une substance radioactive
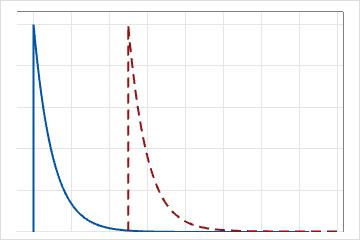
Pour la loi exponentielle à 1 paramètre, le seuil est de zéro et la loi est définie par son paramètre d'échelle. Pour la loi exponentielle à 1 paramètre, le paramètre d'échelle est égal à la moyenne.
Que signifie l'absence de mémoire ?
La loi exponentielle se caractérise essentiellement par son absence de mémoire. La probabilité d'occurrence d'un événement ne dépend pas des essais précédents. De ce fait, le taux d'occurrence reste constant.
Cette absence de mémoire indique que la durée de vie restante d'un composant ne dépend pas de l'âge qu'il a actuellement. Une série de lancers de pièce aléatoires est un exemple d'essais avec absence de mémoire. Un système exposé à une usure normale et qui présente de ce fait un plus grand risque de défaillances pour la suite n'est pas sans mémoire.
Loi gamma
La loi gamma permet de modéliser des valeurs positives qui sont approximativement asymétriques vers la droite et supérieures à 0. Elle est souvent utilisée dans les études de fiabilité/survie. Par exemple, elle permet de décrire le temps avant défaillance d'un composant électrique. La plupart des composants électriques d'un type particulier tombent en panne à peu près au même moment, mais certains mettent plus de temps.
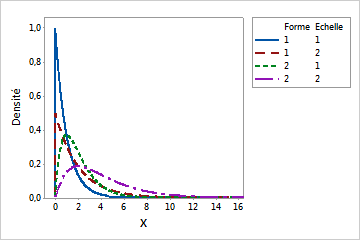
Lorsque le paramètre de forme est un entier positif, la loi gamma est parfois appelée loi d'Erlang. La loi d'Erlang est fréquemment utilisée dans le domaine de la théorie des files d'attente.
Loi de distribution logistique
Utilisez la loi logistique pour modéliser des lois de données dont les extrémités sont plus longues et les aplatissements plus élevés que dans la loi normale.
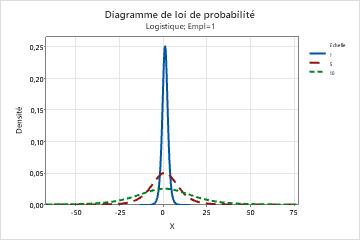
- Effet sur le paramètre d'échelle
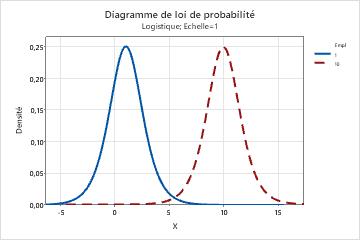
- Le graphique suivant illustre l'effet de différentes valeurs de paramètre d'échelle sur la loi de distribution logistique.
- Effet du paramètre d'emplacement
- Le graphique suivant illustre l'effet de différentes valeurs de paramètre d'emplacement sur la loi de distribution logistique.
Loi log-logistique
Utilisez la loi log-logistique lorsque le logarithme de la variable est distribué de manière logistique. Par exemple, la loi log-logistique est utilisée pour les modèles de croissance et pour modéliser des réponses binaires dans des domaines tels que la biostatistique et l'économie.
La loi log-logistique est une loi de distribution continue définie par ses paramètres d'emplacement et d'échelle. La loi log-logistique à 3 paramètres est définie par ses paramètres d'emplacement, d'échelle et de seuil.
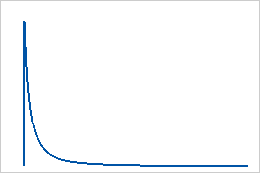
La loi log-logistique est également connue sous le nom de loi de Fisk.
Loi log-normale
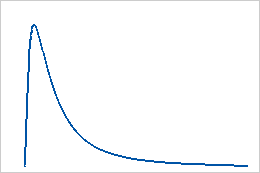
Utilisez la loi log-normale si le logarithme d'une variable aléatoire suit une loi normale. Utilisez-la lorsque les variables aléatoires sont supérieures à 0. La loi log-normale est souvent utilisée dans le cadre d'analyses de fiabilité et dans le domaine de la finance, pour modéliser le comportement d'actions par exemple.
La loi log-normale est une loi de distribution continue définie par ses paramètres d'emplacement et d'échelle. La loi log-normale à 3 paramètres est définie par ses paramètres d'emplacement, d'échelle et de seuil.
Loi normale
La loi normale est une loi de distribution continue caractérisée par la moyenne (μ) et l'écart type (σ). La moyenne est le pic (ou centre) de la courbe en cloche. L'écart type détermine la dispersion de la loi.
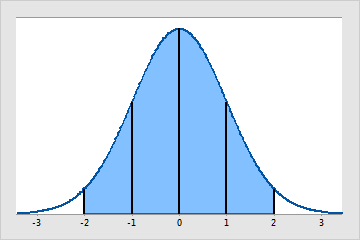
La loi normale est la distribution statistique la plus couramment utilisée car la normalité apparaît naturellement dans de nombreux contextes de mesure (physique, biologique et social). De nombreuses analyses statistiques supposent que les données proviennent de populations suivant approximativement une loi normale.
Lois de distribution des plus grandes et des plus petites valeurs extrêmes
Les lois de distribution des plus grandes et des plus petites valeurs extrêmes sont étroitement liées. Par exemple, si X suit une loi des plus grandes valeurs extrêmes, −X suit une loi des plus petites valeurs extrêmes, et vice versa.
Loi des plus petites valeurs extrêmes
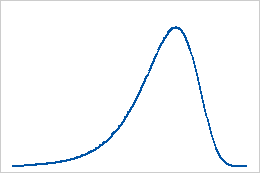
Loi des plus grandes valeurs extrêmes
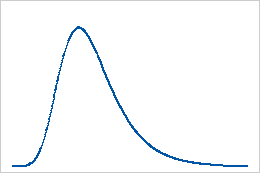
Loi de Weibull
La loi de Weibull est une loi de distribution polyvalente ayant de nombreuses applications dans les domaines de l'ingénierie, de la recherche médicale, du contrôle de la qualité, des finances et de la climatologie. Par exemple, elle est fréquemment utilisée dans le cadre des analyses de fiabilité pour modéliser la durée de fonctionnement avant défaillance. La loi de Weibull permet également de modéliser les données de processus asymétriques dans les analyses de capabilité.
La loi de Weibull est caractérisée par ses paramètres de forme, d'échelle et de seuil, et est également connue sous le nom de loi de Weibull à 3 paramètres. Lorsque le paramètre de seuil est nul, on parle de "loi de Weibull à 2 paramètres". La loi de Weibull à 2 paramètres est uniquement définie pour des variables positives. Une loi de Weibull à 3 paramètres peut fonctionner avec des données nulles et négatives, mais toutes les données d'une loi de Weibull à 2 paramètres doivent être positives.
La loi de Weibull peut prendre diverses formes selon la valeur de ses paramètres.
- Effet du paramètre de forme
- Le paramètre de forme décrit le mode de distribution de vos données. Une forme de 3 produit une courbe presque normale. Une valeur de forme faible (par exemple 1) donne une courbe asymétrique à droite. Une valeur de forme élevée (par exemple 10) donne une courbe asymétrique à gauche.
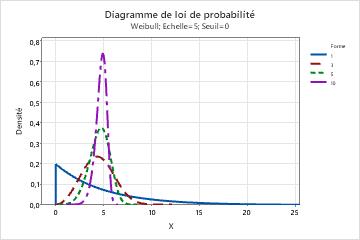
- Effet du paramètre d'échelle
- L'échelle, ou durée de vie caractéristique, correspond au 63,2e percentile des données. L'échelle définit la position de la courbe de Weibull par rapport au seuil, de la même façon que la moyenne définit la position d'une courbe normale. Une échelle de 20, par exemple, indique que 63,2 % de l'équipement tombera en panne dans les 20 heures suivant le moment seuil.
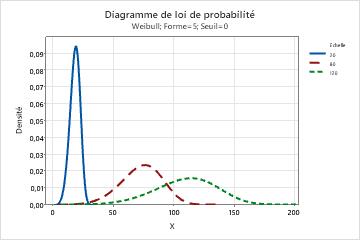
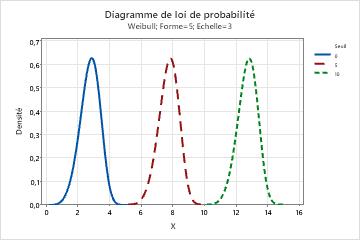
- Effet du paramètre de seuil
- Le paramètre de seuil décrit le décalage de la loi par rapport à 0. Un seuil négatif décale la distribution vers la gauche, tandis qu'un seuil positif décale la distribution vers la droite. Toutes les données doivent être supérieures à la valeur de seuil. La loi de Weibull à 2 paramètres est semblable à la loi de Weibull à 3 paramètres, mais avec un seuil de 0. Par exemple, une loi de Weibull à 3 paramètres (3,100,50) a la même forme et la même dispersion qu'une loi de Weibull à 2 paramètres (3,100), mais est décalée de 50 unités vers la droite.